Позиционные задачи

К позиционным относятся задачи на:

• принадлежность;

• взаимное расположение;

• пересечение.

Задачи на принадлежность (Рис.15) и взаимное расположение были

рассмотрены выше.

Задачи на пересечение необходимо разделить на две большие группы:

1. пересечение линии и поверхности – первая главная позиционная задача (1-я ГПЗ);

2. пересечение двух поверхностей – вторая главная позиционная задача (2-я ГПЗ).

Правила (порядок, алгоритм) решения главных позиционных задач

существенно зависят от расположения пересекающихся геометрических образов относительно плоскостей проекций (занимают общее или проецирующее положение по отношению к плоскости проекций).

Решение главных позиционных задач

1. Оба пересекающихся геометрических образа занимают

проецирующее положение (1-й алгоритм решения):

1-я ГПЗ – пересечение линии и поверхности.

Результатом пересечения линии и поверхности будет точка (или точки), которые одновременно принадлежат обоим пересекающимся Г. О. (линии и поверхности).

Пример 1. Пересечение фронтально проецирующей прямой n и горизонтально проецирующей плоскости  (Рис.37):

n х  = А = ? n  II1 и  П2;

n2 - главная (вырожденная) проекция прямой п на П2;

1 - главная (вырожденная) проекция плоскости  на П1;

Ниже приводится порядок (алгоритм) решения таких задач.

1. На П1 и П2 выделяем общие зоны существования проекций пересекающихся Г.О. (точка).

2. Обозначаем точку А (результат пересечения) в пределах выделенных зон.

А2 = n2 и А1 = n1 х 1.

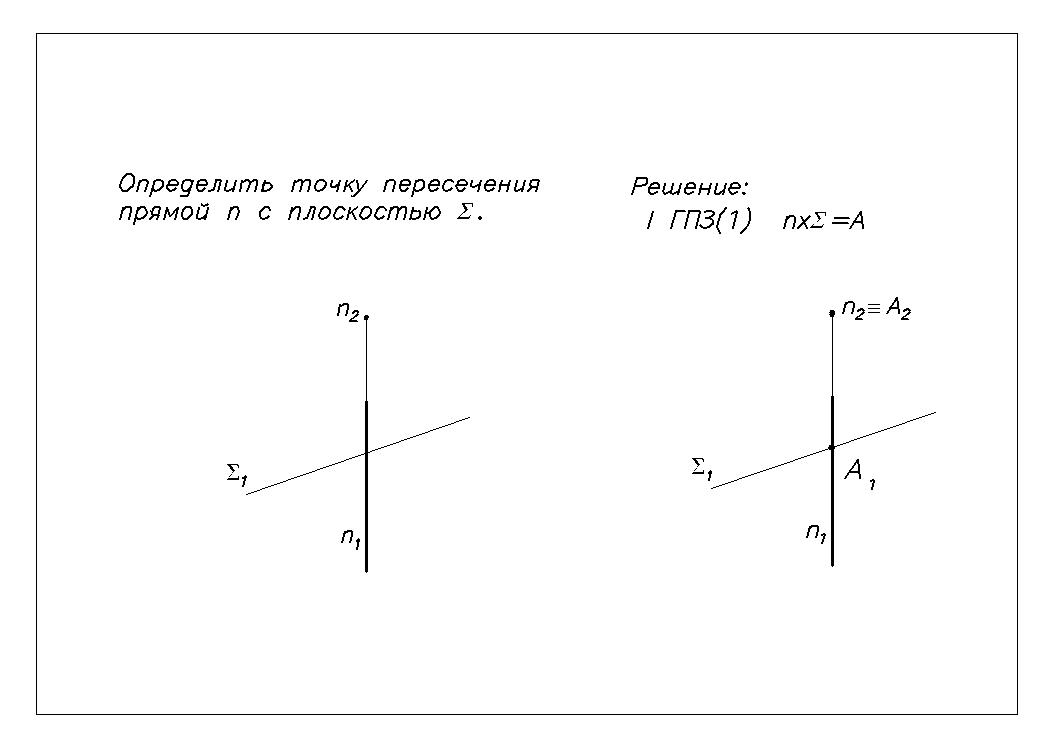
Рис.37

Проекции точки пересечения (А1, А2) на плоскостях проекций П1 и П2

совпадают с главными проекциями геометрических образов, занимающих проецирующее положение по отношению к соответствующим плоскостям проекций.

Пример 2 Пересечение фронтально проецирующей прямой n с поверхностью горизонтально проецирующего кругового цилиндра  (Рис.38).

n х  = А,А = ? n  II2 и  П1;

n2 - главная (вырожденная) проекция прямой п на П2;

1 - главная (вырожденная) проекция кругового цилиндра  на П1;

Решение задачи аналогично решению, приведенному в примере 1.

Рис.38

2–я ГПЗ – пересечение двух поверхностей.

Результатом пересечения двух поверхностей будет линия (или линии), точки которых одновременно принадлежат обеим поверхностям.

Пример 1. Пересечение фронтально проецирующей плоскости  с поверхностью горизонтально проецирующего кругового цилиндра  (Рис.39)

 х  = m = ?;   П2; П1.

2 - главная (вырожденная) проекция плоскости  на П2;

1 - главная (вырожденная) проекция кругового цилиндра  на П1;

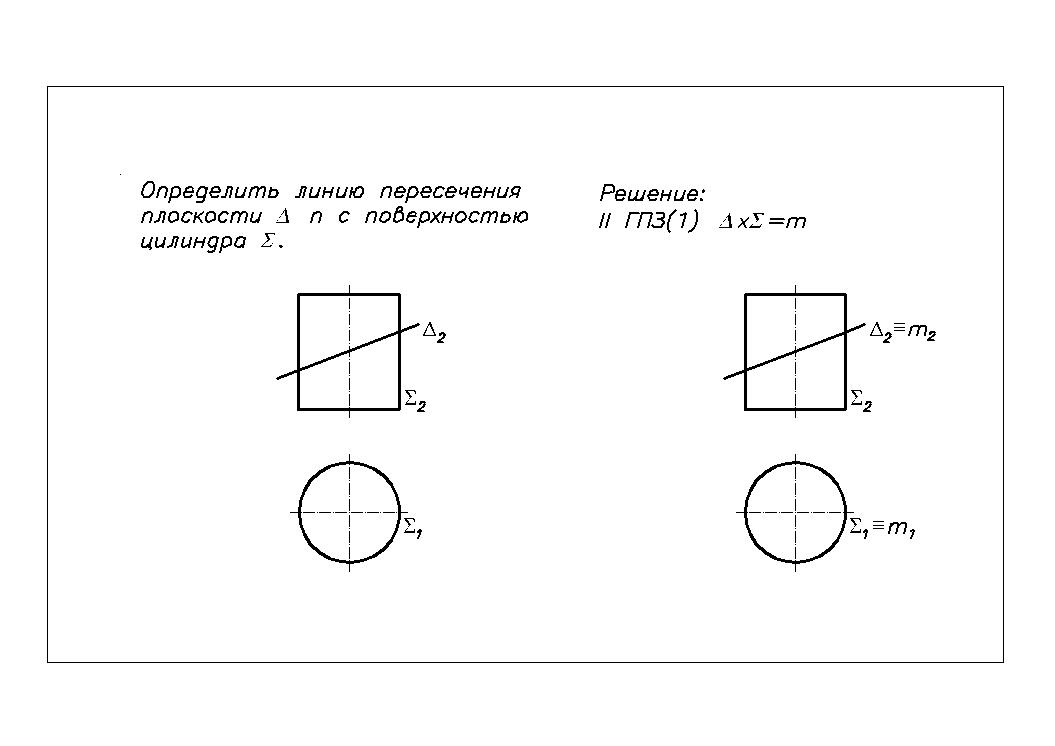
Рис.39

На обеих плоскостях проекций определяем общие зоны существования проекций пересекающихся геометрических образов, в которых и расположены проекции линий пересечения поверхностей  и .

На П1 проекция линии пересечения (m1) совпадает с главной проекцией поверхности  (m1 = 1);

На П2 проекция линии пересечения представляет собой фрагмент проекции  ограниченный контурными образующими поверхности .

Пример 2 Пересечение поверхности фронтально проецирующего кругового цилиндра  с поверхностью горизонтально проецирующего кругового цилиндра  (Рис.40).

 х  = n = ?   II2 и  П1;

2 - главная (вырожденная) проекция кругового цилиндра  на П2;

1 - главная (вырожденная) проекция кругового цилиндра  на П1;

Решение задачи аналогично решению, приведенному в примере 1 (Рис.).

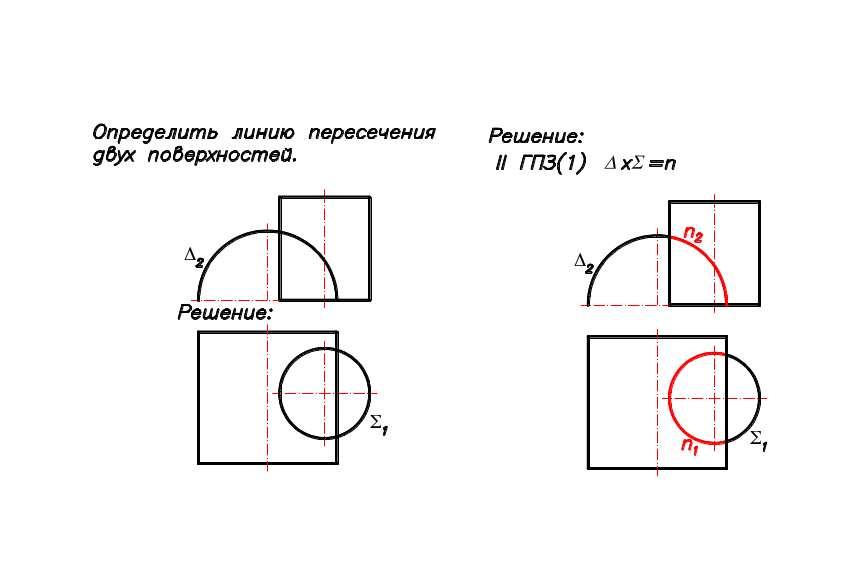
Рис.40