Лекция 2. . Задание линии на комплексном чертеже. Задание плоскости на к.Ч.
Комплексный чертеж линии.
Линия - это геометрический образ, сформированный последовательным перемещением точки при ее движении по определенному закону.
Линия – одномерный геометрический образ.
Обозначение линий – a, b, c, d … и т.д.
Линии бывают:
в зависимости от закона, описывающего движение точки:
прямые;
кривые;
ломаные;
2. плоские и пространственные;
3. в зависимости от вида описывающего уравнения:
алгебраические;
трансцендентные.
На рис. 7 приведен комплексный чертеж прямой АВ. Прямая однозначно задана на комплексном чертеже, если заданы две ее проекции. На чертеже не задана ось Х. В этом нет необходимости. Положение оси Х никак не влияет на результаты при решении различных задач.
Взаимное расположение двух прямых.
Параллельные прямые
Две прямые параллельны между собой, если их одноименные проекции тоже параллельны (Рис.8).
Если a II b, то a1 II b1 и a2 II b2.
Рис.8
П
ересекающиеся
прямые (имеют одну общую точку).
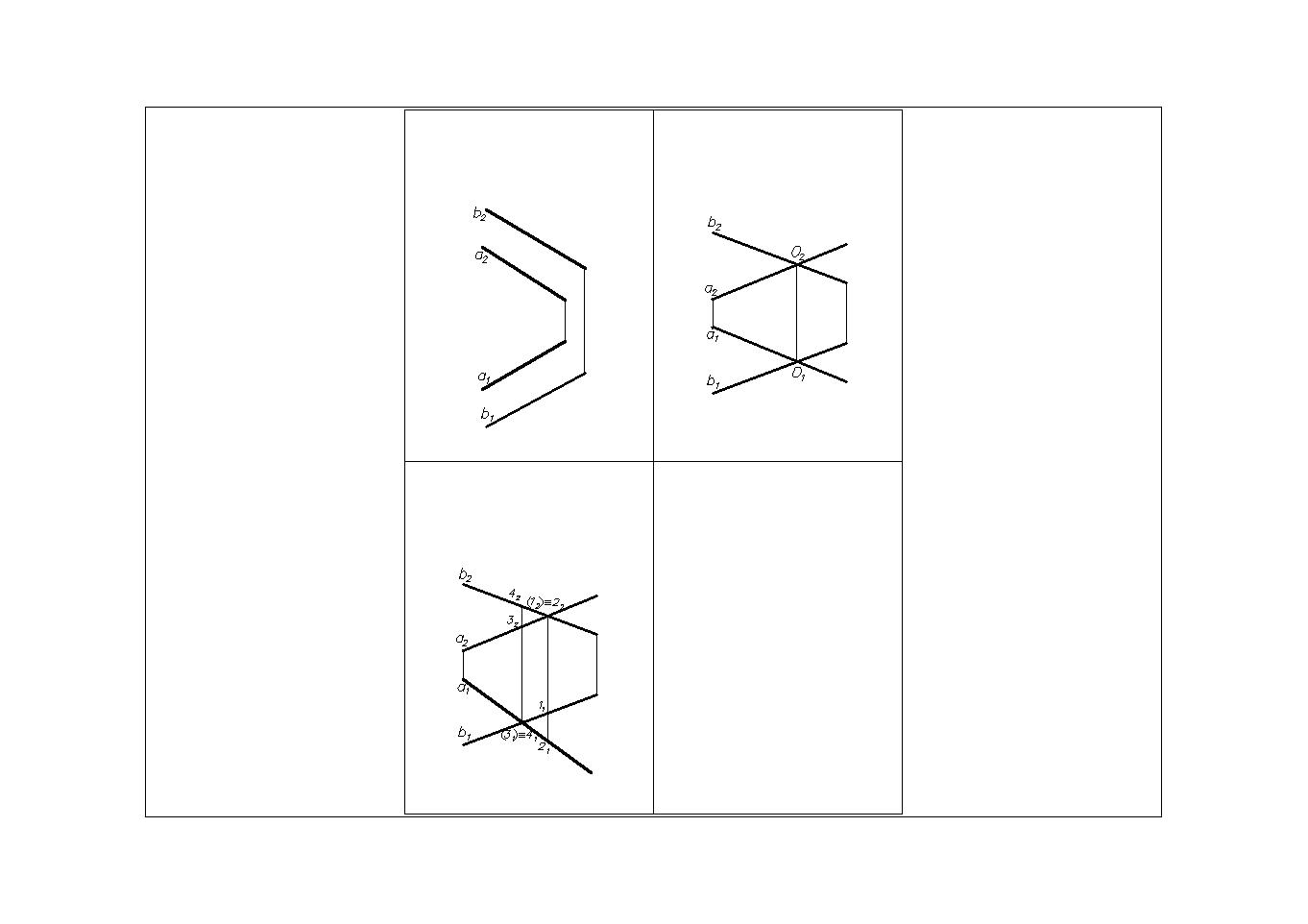
Две прямые пересекаются между собой, если точки пересечения одноименных проекций прямых лежат на одной линии связи (Рис.9).
a x b = О;
a1 x b1 = О1;
a2 x b2. = О2.
Рис.9
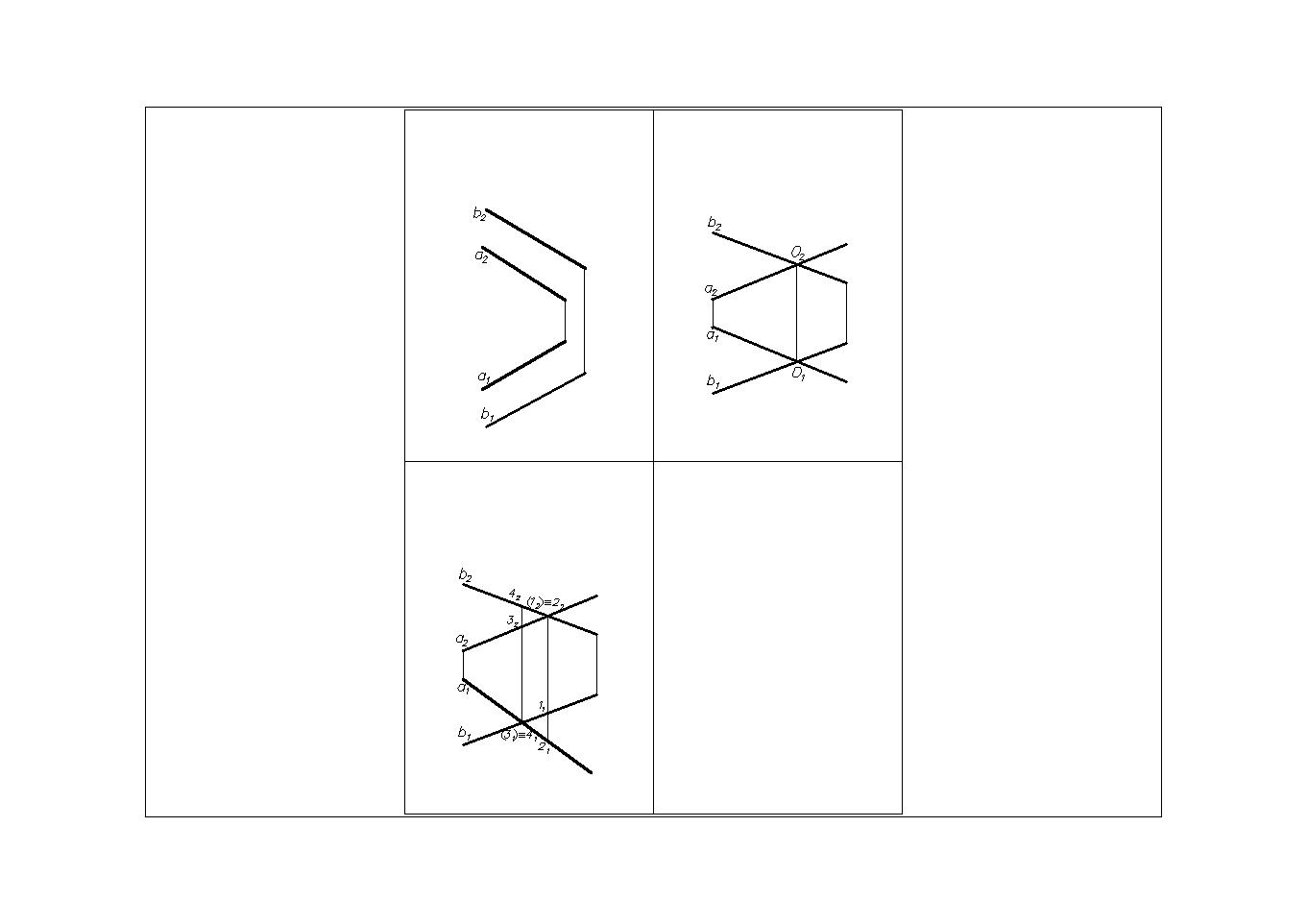
Скрещивающиеся прямые (не имеют общих точек).
Две прямые скрещиваются между собой, если точки пересечения их одноименных проекций лежат на разных линиях связи (Рис.10).
Рис.10
Положение прямых линий относительно плоскостей проекций.
Введем новое понятие – профильная плоскость проекций (П3). Это плоскость, которая одновременно перпендикулярна (ортогональна) к плоскостям П1 и П2.
В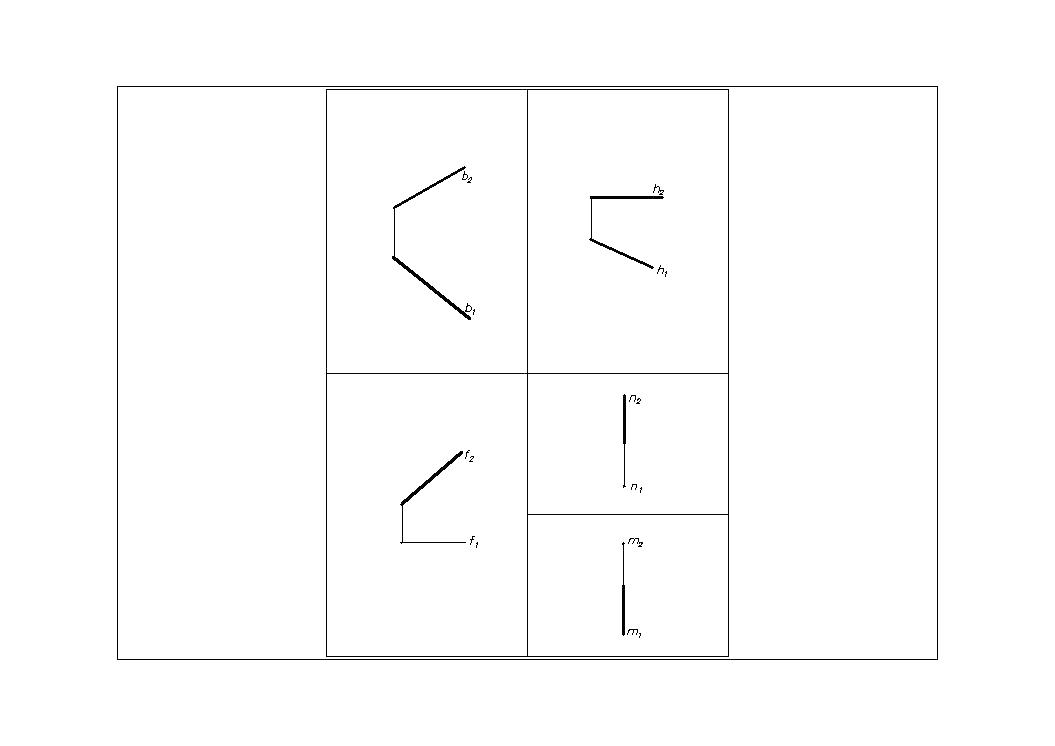
зависимости от своего положения
относительно плоскостей проекций прямые
разделяют на прямые
общего положения
и прямые
частного положения.
Прямая общего положения (Рис.11)– прямая, которая имеет углы, отличные от 0 и 90 одновременно со всеми тремя плоскостями проекции (П1, П2 и П3).
Рис.11
Прямые, которые параллельны плоскостям проекций или перпендикулярные к ним называются прямыми частного положения.
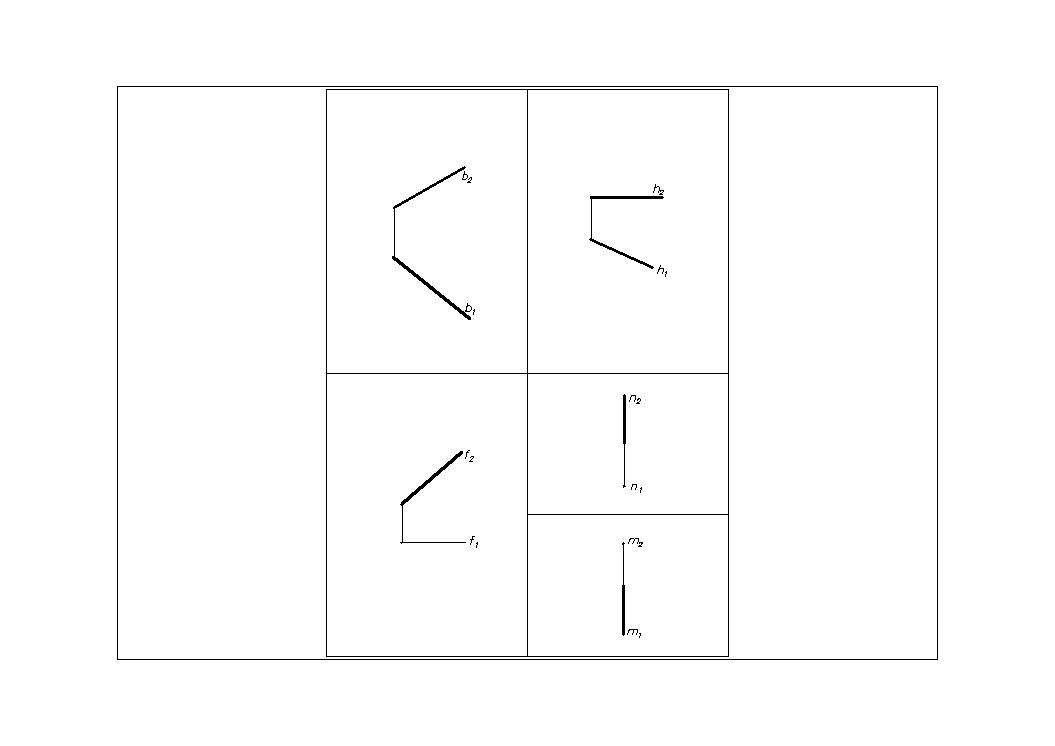
Линии уровня.
Горизонталь – линия, все точки которой имеют одинаковую координату Z (аппликата) . Рис.12
Горизонталь параллельна горизонтальной плоскости проекций.
Обозначение горизонтали – h (h II П1).
Рис.12
На П2 - Z– const (для всех точек линии).
На П1: h1=h, h1 - натуральная величина прямой h.
Ф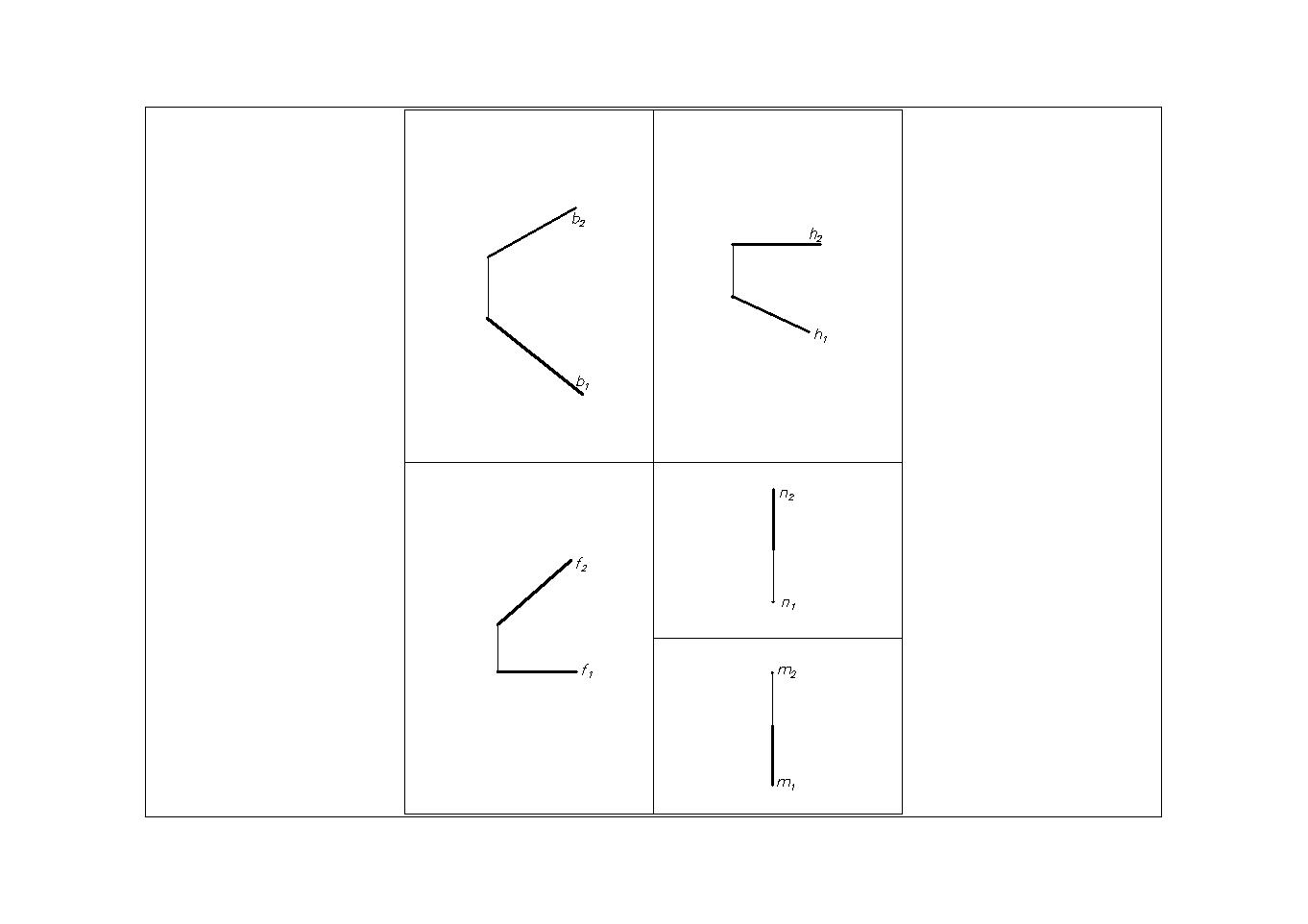
ронталь–
линия,
все точки которой имеют одинаковую
координату Y
(ордината). Рис.13
Фронталь параллельна фронтальной плоскости проекций.
Обозначение фронтали – f (f II П2).
На П1 - Y – const (для всех точек прямой)
На П2 f2 = f, f2 - натуральная величина отрезка АВ.
Рис.13
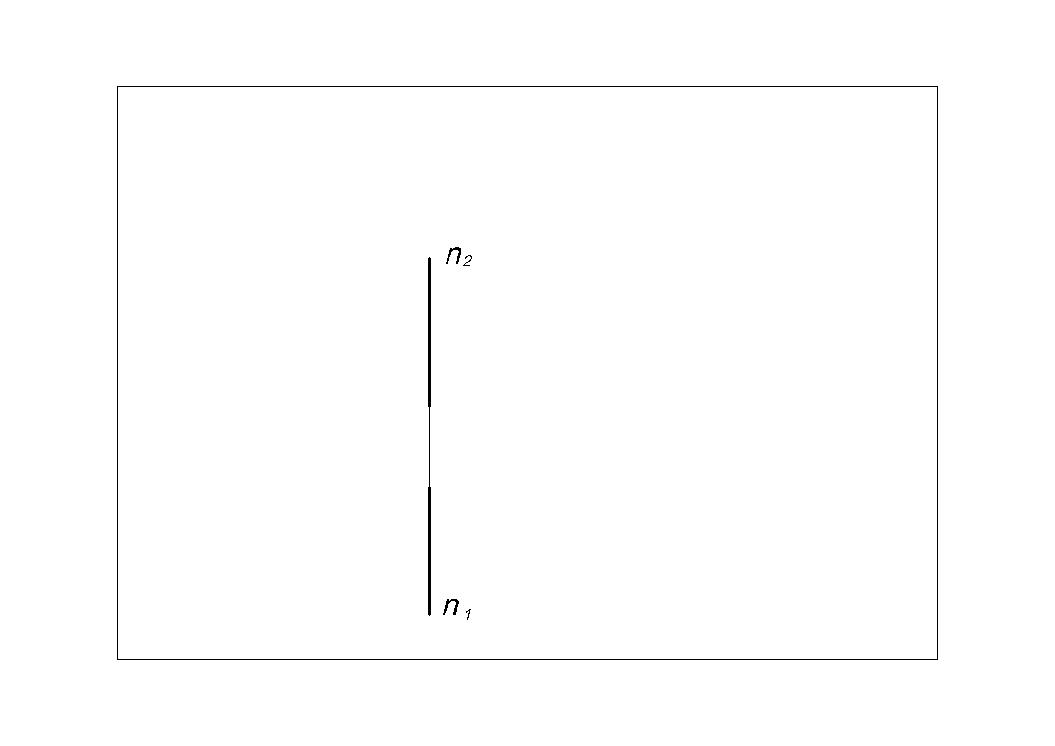
Профильная линия – линия, все точки которой имеют одинаковую координату X (абсцисса).
Профильная (Рис.14) линия параллельна профильной плоскости проекций. Обозначим профильную линию буквой п (п II П3). На П1 и П2 проекции профильной линии п совпадают с линией связи. Для описания профильной линии (прямой) на комплексном чертеже необходимо вводить профильную плоскость проекций.
Рис.14