Кухарчук А.И.

Курс лекций по дисциплине «Начертательная геометрия»

1-й курс; Специальности ИМБ, ИДБ, ИХС, ИСБ, ИАБ

36 Часов; 18 лекций

Лекция 1.

Виды проецирования. Задание точки на комплексном чертеже

Предмет «Начертательная геометрия» (Н.Г.) изучает законы отображения трехмерного пространства на двумерную плоскость методами проекций и сечений.

Перед Н.Г. стоят две основные задачи:

1. прямая – построить изображение пространственного предмета на чертеже;

2. обратная – реконструкция пространственного предмета по чертежу.

Сущность метода проекций.

Построение любого изображения выполняется с помощью операции проецирования. Проецирование заключается в следующем:

(Рис.1) в пространстве выбирают произвольную точку S (центр проецирования) и плоскость П1 (плоскость проекций или картинная плоскость). Чтобы спроецировать точку пространства А на плоскость П1, через вершину S проводят прямую а до пересечения с плоскостью

П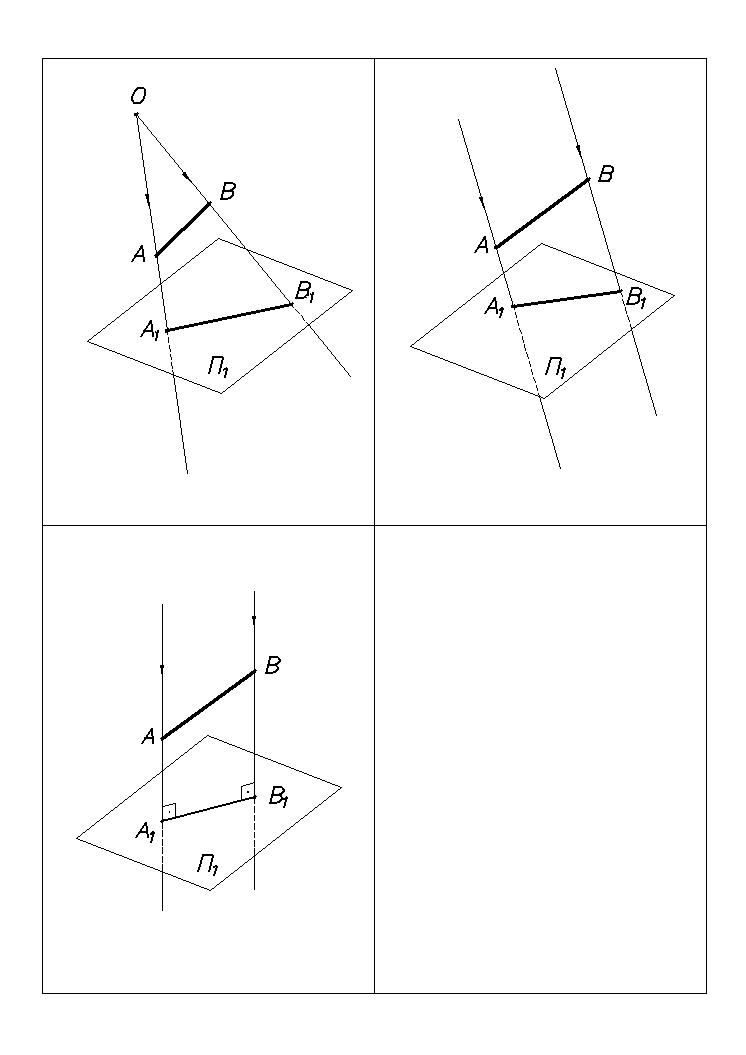 1 в точке А1. Точку А1 принято называть центральной проекцией точки А на плоскость П1. Проекцией фигуры называется множество проекций всех ее точек. Такой вид проецирования называется линейным центральным проецированием ( Л.Ц.П.)

Л.Ц.П. обладает большой наглядностью, т.к. процесс человеческого зрения в геометрическом отношении совпадает с операцией центрального проецирования.

В машиностроении практически не применяется, т.к. нет закономерных отношений между линейными размерами геометрического образа (Г.О.) и его проекциями.

Рис.1

Параллельное проецирование

Проецирование, при котором центр проекций удален в бесконечность, называется параллельным (Рис.2).

При параллельном проецировании проецирующие прямые параллельны между собой. Угол наклона прямых к плоскости П1 от 0 до 90 .

Мало применяется в машиностроении по той же причине, что и центральное проецирование.

Рис.2

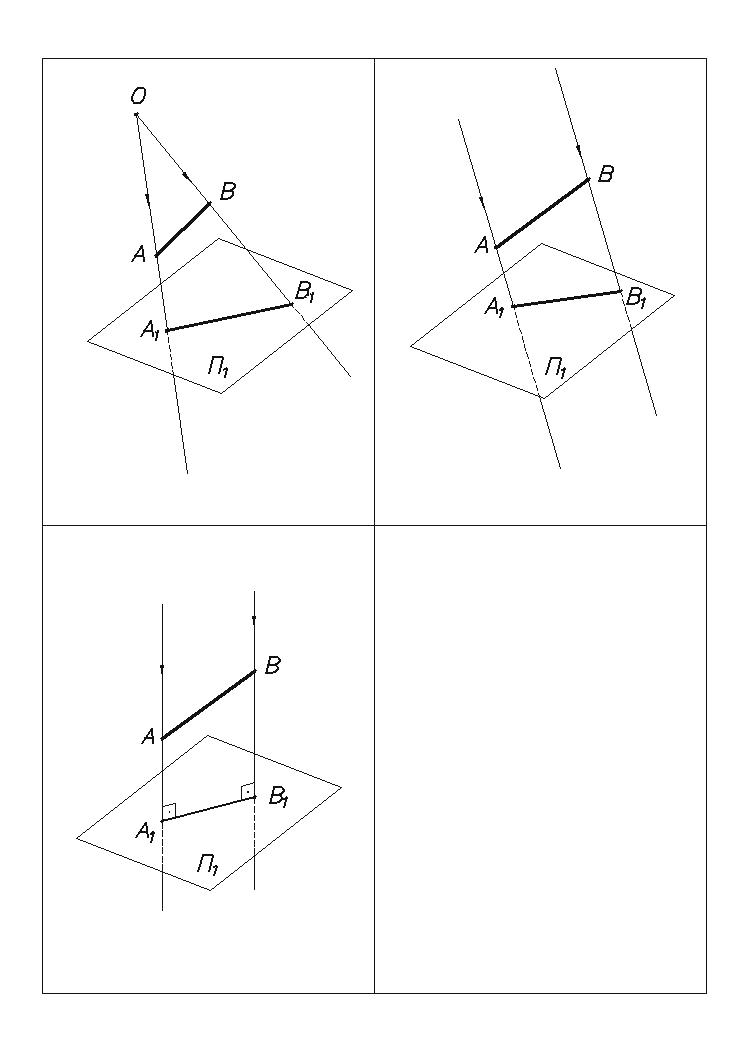
Ортогональное проецирование

(частный случай параллельного проецирования).

В этом случае проецирующие прямые (Рис.3) перпендикулярны (ортогональны) плоскости проекций П1 (s  П1). Этот вид проецирования и применяется при выполнении машиностроительных чертежей.

Рис.3

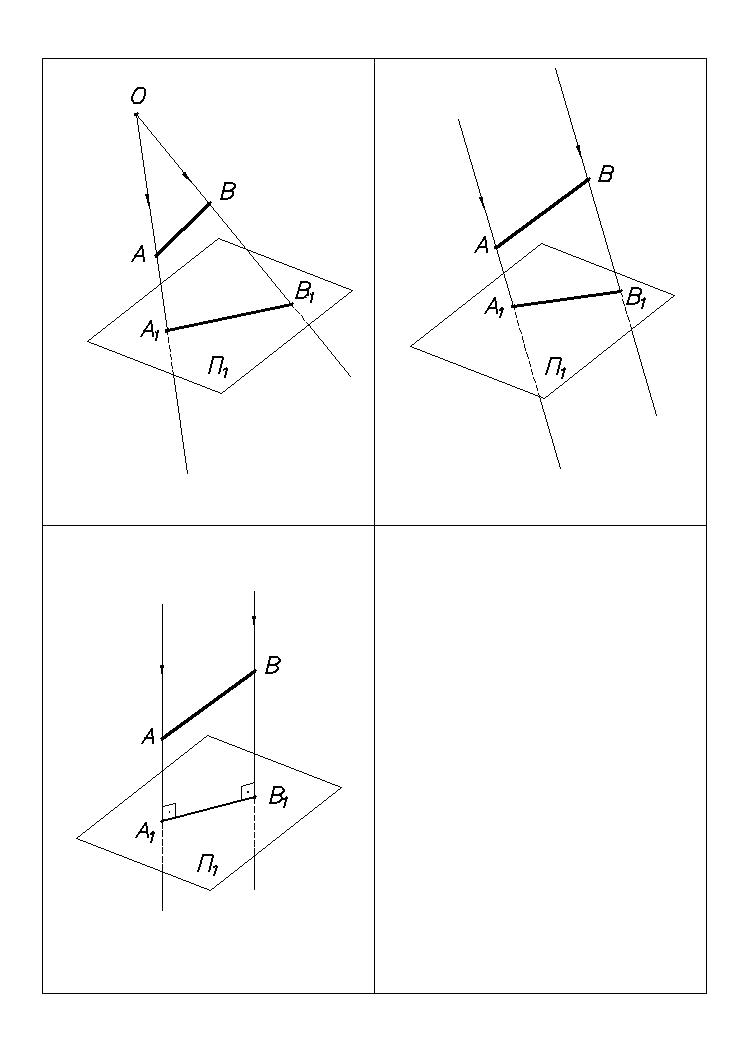
Свойства ортогонального проецирования.

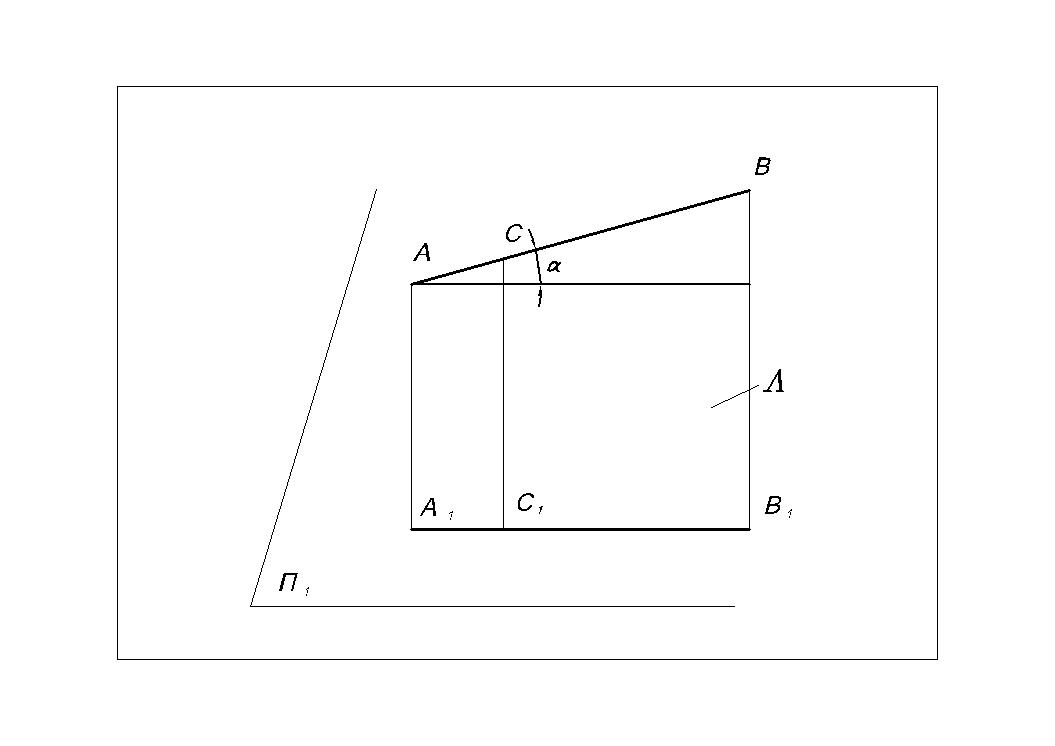
а) Позиционные свойства (Рис.4):

1. каждой точке проецируемого Г.О. соответствует одна точка на плоскости проекций,

А  А1;

(обратная зависимость неоднозначна);

2. проекцией прямой линии АВ является прямая линия А1В1,

АВА1В1; АВА1В1– проецирующая плоскость L);

3. если точка принадлежит линии, то ее проекция принадлежит проекции данной линии,

С  АВ  С1  А1В1;

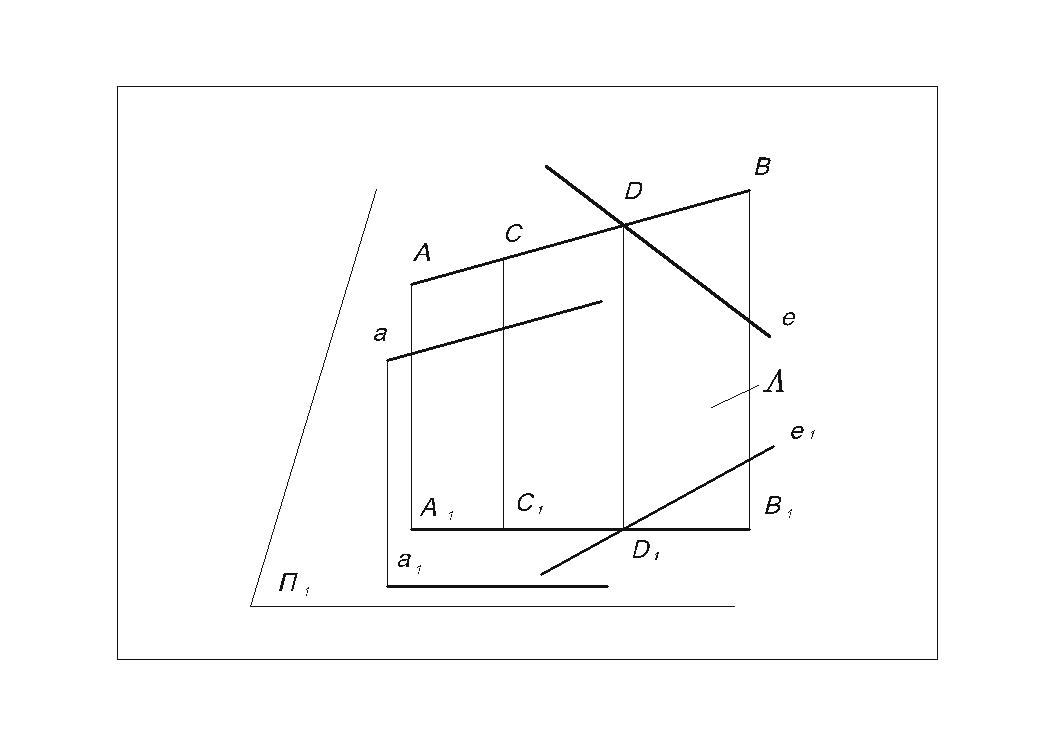
Рис.4 4. проекцией точки пересечения двух прямых является точка пересечения проекций данных прямых;

D = АВ х е  D1 = А1 В1 х e1;

5. проекциями двух параллельных прямых являются две параллельные прямые,

а II AB  а1 II А1 В1;