
Простые операции
Арифметические и логические операции Matlab
Символ операции |
Выполняемое действие |
+ |
Покомпонентное сложение числовых массивов одинаковой размерности; Добавление скалярной величины к каждому элементу массива; Сложение скалярных величин; |
- |
Покомпонентное вычитание числовых массивов одинаковой размерности; Вычитание скалярной величины к каждому элементу массива; Вычитание скалярных величин; |
* |
Умножение матриц в соответствии с правилами линейной алгебры (число столбцов первого сомножителя должно быть равно числу строк второго сомножителя); Умножение всех компонент вектора на скаляр; Умножение скаляра на скаляр; |
/ |
Деление скаляра на скаляр; Покомпонентное деление всех элементов массива на скаляр: A / B = A*B-1 = A* inv(B) (A,B – квадратные матрицы одного порядка); |
. / |
Покомпонентное деление элементов массивов одинаковой размерности; |
\ |
A \ B = A-1*B (левое матричное деление, А – квадратная матрица) |
. \ |
A.\B – покомпонентное деление элементов B на А (левое поэлементное деление); |
^ |
Возведение скаляра в любую степень; Вычисление целой степени квадратной матрицы; |
‘ |
Вычисление сопряженной матрицы; |
.’ |
Транспонирование матрицы; |
^-1 |
Вычисление обратной величины скаляра; A^-1 - Вычисление обратной матрицы (A-квадратная матрица); |
|
Логические операции |
& (and) |
Логическое умножение скаляров; Логическое покомпонентное умножение массивов одинаковой размерности; |
| (or) |
Логическое сложение скаляров; Логическое покомпонентное умножение массивов одинаковой; Логическое сложение массива со скаляром; |
~ (not) |
Логическое отрицание скаляра или всех элементов массива; |
Xor |
Логическое исключающее или |
== |
Проверка на равенство |
~= |
Проверка на не равенство |
> |
Проверка на «больше» |
>= |
Проверка на «больше или равно» |
< |
Проверка на «меньше» |
<= |
Проверка на «меньше или равно» |
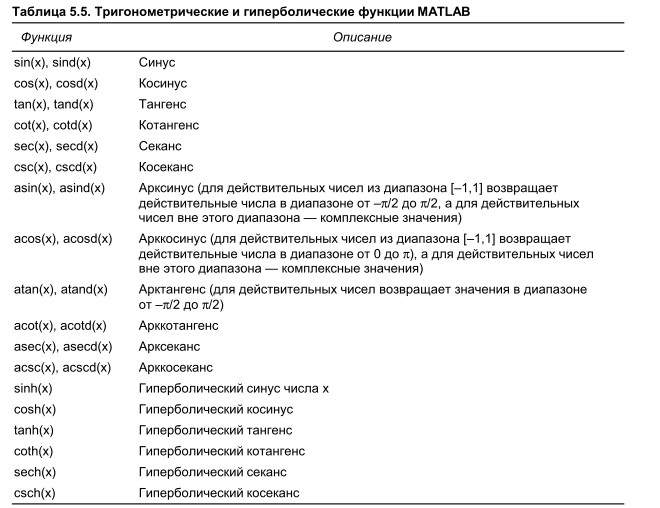
Элементарные алгебраические функции
Функция |
Описание |
abs(z), abs(x), |
Вычисление модуля комплексного числа z или абсолютного значения действительного числа x. |
angle(z) |
Вычисление аргумента z. |
sqrt(z), sqrt(x) |
Вычисление квадратного корня чисел z и x |
real(z) |
Вычисление действительной части комплексного числа z. |
imag(z) |
Вычисление мнимой части комплексного числа z. |
round(x) |
Округление до целого. |
fix(x) |
Округление до ближайшего целого в сторону нуля. |
rem(x, y) |
Вычисление остатка от деления x на y. |
exp(z) |
Вычисление е в степени x. |
log(z) |
Вычисление натурального логарифма числа x. |
log10(z) |
Вычисление десятичного логарифма числа x. |
Для проведения аналитических операций, таких как дифференцирование, интегрирование и т.д. необходимо соответствующие переменные предварительно объявить как символьные. Группу символьных переменных создаёт команда syms, например:
>> syms s1 s2
Интегрирование
Интеграл вычисляет функция int().
Пример.
Вычислить неопределённый интеграл от
функции
 .
.
>> syms x k
>> s=int(x^k,x)
s =
x^(k+1)/(k+1)
Дифференцирование
Дифференцирование выполняет функция diff(). По умолчанию дифференцирование производится по x, при дифференцировании по другим переменным их надо явно указывать.
Пример.
Определить функцию
 и найти её производные первого порядка
по x
и по y.
и найти её производные первого порядка
по x
и по y.
>> f=x^2/(1+y^3)^(1/2)+y*sin(x);
>> diff(f)
ans =
2*x/(1+y^3)^(1/2)+y*cos(x)
>> diff(f,y)
ans =
-3/2*x^2/(1+y^3)^(3/2)*y^2+sin(x)
Вычисление пределов
Предел вычисляет функция limit().
Пример.
Найти
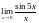 .
.
>> limit(sin(5*x)/x,x,0)
ans =
5
Для обозначения левого и правого пределов испольэуются слова 'left' и 'right'.
