12. Расчет плоских рам на устойчивость.
Для статически неопределимой рамы требуется определить значения критических сил, используя метод перемещений.
Дано:
|
Решение:
|
Найти:
|
1. Вычисляем аргументы для стоек по формуле:
Левая стойка
Правая стойка
2. Определяем соотношения погонных жесткостей стрежней рамы по формуле:
,
3. Определяем степень кинематической неопределимости и выбираем основную систему
следовательно, рама дважды кинематически
неопределима.
4. Составляем систему канонических уравнений:
5. Строим единичные эпюры изгибающих моментов, используя таблицу реактивных усилий от единичных смещений.
,
,
,
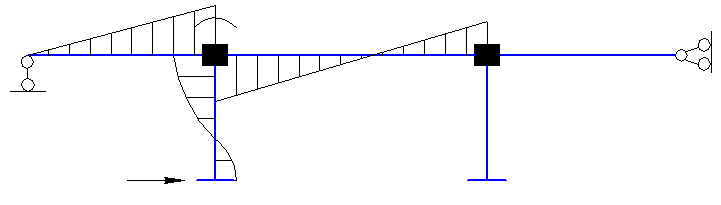
Реакция
,
,
,
Реакция
,
,
,
Реакция ,
,
,
Реакция
6. Определяем коэффициенты канонических уравнений по правилу «что-где»
так как - узловое неизвестное, вырезаем узел в первой единичной эпюре
|
|
так как - узловое неизвестное, вырезаем узел во второй единичной эпюре
|
|
так как - узловое неизвестное, вырезаем узел во второй единичной эпюре
|
|
7. Составляем уравнение устойчивости.
Метод попыток
,
,
,
,
,
,
Выбираем
,
,
8. Определяем критическую нагрузку
Для левой стойки
Для правой стойки
13. Динамический расчет плоских рам.
Для плоской рамы требуется
1) определить круговую частоту свободных вертикальных и горизонтальных колебаний, приняв раму как систему с двумя степенями свободы (собственный вес системы не учитывается)
2) определить динамическое воздействие
вертикальной вибрационной силы
а) принять частоту вертикальной
возмущающей силы
равной половине минимальной частоты
собственных колебаний.
б) определить динамический коэффициент
в) построить эпюру изгибающих моментов с учетом динамического воздействия силы Р.
Дано:
|
Решение:
|
Найти:
Эпюра М - ? |
1. Анализируем конструкцию.
рама статически определимая.
Конструкция имеет 2 степени свободы.
2. Строим единичные эпюры изгибающих моментов от единичных сил инерции.
Единичные силы инерции прикладываем по направлению возможных колебаний.
|
Найдем реакции:
|
,
|
Найдем реакции:
,
|
3. Составляем вековое уравнение
Определяем единичные коэффициенты от единичных сил инерции по правилу Верещагин
4. Решаем вековое уравнение примет вид
первый корень
- основной тон колебаний.
второй корень
- первый обертон
5. Определяем динамический коэффициент колебаний с учетом действия на конструкцию вибрационной нагрузки
6. Строим окончательную эпюру изгибающих моментов с учетом вертикальной возмущающей силы
