Теория вероятностей и математическая статистика случайные события

Случайными событиями называются такие события, которые могут произойти или не произойти при осуществлении совокупности условий, связанных с возможностью появления данных событий.

Каждое осуществление рассматриваемой совокупности условий называется испытанием. Отношение числа “m” наступлений данного случайного события А в данной серии испытаний к общему числу испытаний этой серии “n” называется частотой появления события А в данной серии испытаний или частотой события А и обозначается:

.

Частота случайного события всегда заключена между нулем и единицей :

0 ≤ ≤ 1.

Алгебра событий

Суммой двух событий (обозначается А + В или А U В ) называется событие, состоящее в том, что в результате испытания произойдет хотя бы одно из двух событий : или А, или В, или оба одновременно.

Произведением двух событий , А ∩ В (АВ), называется событие, состоящее в том, что в результате испытания произойдут оба события и А, и В.

Противоположным к событию А ( обозначается А ) называется событие, состоящее в том, что в результате испытания событие А не произойдет.

События А и В называются несовместимыми, если появление одного события исключает появление другого в одном и том же испытании.

События А₁, А₂, А₃, ... , А_n образуют полную группу событий, если они попарно несовместны и сумма этих событий есть достоверное событие А₁ + А₂ + А₃ + ... + А_n = U.

Элементарная группа событий

События ε₁, ε₂, ..., ε_n образуют элементарную группу событий, если выполняются условия:

1. Эти события образуют полную группу событий;

2. Эти события равновозможные.

Классическое определение вероятности

Пусть возможные результаты испытания можно представить в виде “n” единственно возможных, несовместных друг с другом и равновозможных элементарных исходов (случаев), т.е. результаты испытания образуют элементарную группу событий. И пусть “m” из этих исходов связаны с наступлением события А (благоприятствуют событию А). За вероятность события А в этом случае принимают отношение :

,

где n - число возможных элементарных исходов испытания;

m - число элементарных исходов испытания, благоприятствующих появлению события А.

Задача № 8

В ящике имеется N₁ деталей. Из них m - бракованных. Наудачу извлечем 4 детали. Найти вероятность того, что среди извлеченных деталей :

а) нет стандартных;

б) две стандартных и две бракованных;

а) n - число всех возможных вариантов. Извлечь 4 детали .

m₁ - число всех возможных вариантов, что среди извлеченных нет стандартных,

m₂ = С ­_m⁴ , тогда вероятность того, что среди 4 деталей нет стандартных :

;

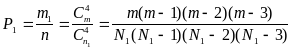б) m₃ - число всех возможных вариантов, что среди 4 деталей две стандартных и две бракованных , тогда вероятность того, что среди 4 деталей две стандартные и две бракованные:

.

Основные теоремы теорема сложения вероятностей

Для несовместимых событий:

Р(А + В) = Р (А) + Р(В);

Р(А + В + С) = Р(А) + Р(В) + Р(С). (1)

Для совместимых событий:

Р(А +В) = Р(А) +Р(В) - Р(А В). (2)

Теорема обобщается на любое число слагаемых.

Следствия:

а) противоположные события А и А несовместимы и сумма их - достоверное событие. Из равенства (1) следует: Р(А) = 1 - Р(А); (3)

б) события А₁, А₂, А₃,..., А_n образуют полную группу событий, если они несовместимы, и в результате данного испытания наступит обязательно одно из них. Для событий, образующих полную группу, справедливо равенство:

Р(А₁) + Р(А₂) + ... + Р(А_n) = 1.