Ряды основные определения

Бесконечная сумма вида (1)

называется рядом.

Сумма (2)

называется n-й частичной суммой ряда (1).

Величина называется суммой ряда (1). (3)

При этом, если предел (3) существует и конечен, то ряд (1) называется сходящимся, в противном случае - расходящимся.

Условие (4)

называется необходимым условием сходимости ряда (1).

Если (4) не выполняется, то ряд (1) расходится. Если (4) выполняется, то (1) может быть как сходящимся, так и расходящимся.

Условия, при выполнении которых (1) сходится, называются признаками сходимости. Приведем некоторые их них, применимые к положительным рядам (т. е. при условии, что U_i - числа и U_i  0 для всех номеров i ).

1. Признак сравнения

Пусть и - два числовых положительных ряда и известно, как ведет себя ряд . Если существует , а так же , то эти два ряда ведут себя одинаково ( т. е. одновременно оба либо сходятся, либо расходятся). При этом учитываем, что ряд (обобщенный гармонический ряд), а так же, что ряд ( как бесконечно убывающая геометрическая прогрессия)

2. Признак сходимости Даламбера

Рассмотрим ряд.

; обозначим Д = .

Если Д =

3. Признак сходимости Коши

Обозначим К = .

Если К =

Задача № 4 Проверить выполнение необходимого условия сходимости:

; ;

(вывод сделать самостоятельно)

Задача № 5 Исследовать положительные ряды с помощью признаков сходимости.

1. ; 2. ; .

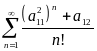1.

Сравним с рядом , который является сходящимся.

Итак, . (вывод сделать самостоятельно).

2. .

Применим признак сходимости Коши, учитывая, что (формула Стирлинга).

(вывод сделать самостоятельно).

Знакочередующиеся ряды

Ряд вида (5)

называется знакочередующимся (как и раньше, U_n  0).

Если при этом ряд (1), т. е. положительный ряд сходится, то ряд (5) называется абсолютно сходящимся.

Если же ряд (1) расходится, а ряд (5) сходится, то (5) называется условно сходящимся.

Приведем один признак условной сходимости ряда (5).

Признак Лейбница

Если у знакочередующегося ряда (5) при n U_n , убывает монотонно и стремится к 0, то (5) сходится.

Заметим, что если (5) сходится абсолютно, то тем более он сходится условно.

Задача № 6 Исследовать на абсолютную и условную сходимость

1. ; 2. .

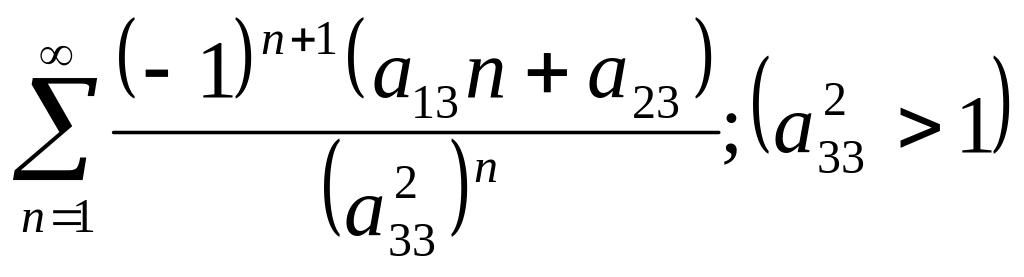1. .

Положительный ряд расходится (показать самостоятельно, пользуясь, например, признаком сравнения). Исходный же ряд удовлетворяет всем условиям признака Лейбница:

1. знаки чередуются, т. к. присутствует множитель (-1)ⁿ⁺¹;

2. (показать самостоятельно);

3. убывает монотонно, т. е. для любого n:

 (также показать самостоятельно).

Итак, исходный ряд сходится условно.

2. .

Положительный ряд сходится (показать самостоятельно, используя признаки сходимости Даламбера или Коши).

Следовательно, исходный ряд сходится абсолютно.