Вопрос 21

. Каков физический смысл коэффициента перекрытия

Для зубчатой передачи очень важную роль играет коэффициент перекрытия. Это один из качественных показателей любой зубчатой передачи. Физический смысл коэффициента перекрытия: число пар зубьев одновременно находящихся в зацеплении. С другой стороны коэффициент перекрытия - величина дробная. Например коэффициент перекрытия равный 1,6 показывает, что в зацеплении всегда находится одна пара зубьев и какое то время, а именно 60% от времени работы зубчатого механизма находятся в зацеплении две пары зубьев. Коэффициент перекрытия влияет на нагрузку зуба по рабочему участку эвольвентного профиля.

Вопрос №25

Диаметр окружности впадин зубьев находим по формуле

df = d -2.5mn = 163 – 2.5*1.5=159.25мм.

Вопрос 26

Диаметры окружностей вершин da и впадин зубьев df: шестерни dal=d1 + 2m; dfl=d1—2,5m; колеса внешнего зацепления da2 = d2 + 2m; df2 = d2 — 2,5m;            (2.24) зацепления da2 = d2 — 2m; df2 = колеса внутреннего = d2 + 2,5m. Ширину шестерни Ъх (мм) принимают по соотношению btlb2, где Ъ2 — ширина колеса: При Ъ2.................... до 30 св. 30 св. 50 св. 80 до 50 до 80 до 100 bjb2           1,1 1,08 1,06 1,05 Полученное значение Ъх округляют до целого числа. В коробках передач ширину шестерни обычно принимают bi = b2. 8.      Пригодность заготовок колес. Чтобы получить при Т. О. принятые для расчета механические характеристики материала, размеры заготовки колес не должны превышать предельно допустимых величин. Значения D3ar, Сзаг, SMr (мм) вычисляют (рис. 2.2): для цилиндрической шестерни D3ar =da + 6 мм; для колеса с выточками принимают меньшее из двух Сзаг = 0,562; S3ar = 8-/w; для сплошного колеса, без выточек (см. рис. 2.2) S3ar = = b2+4 мм. 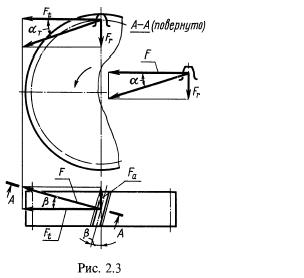Условия пригодности заготовок колес         Предельные значения /)пред и 5пред приведены в табл. 2.1. При невыполнении неравенств изменяют материал дета­лей или вид термической обработки. 9.     Силы в зацеплении (Н) (рис. 2.3): Ft. J.         окружная Ft = 2T2/d2; -А-А(подернуто) радиальная Fr = Fttgα/cosβ;'(2.25) осевая Fa = Ft tg β. Для стандартного угла tga = tg20° = 0,364.

 

Вопрос 6

Зубча́тое колесо́, шестерня́ — основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса. В машиностроении принято малое зубчатое колесо с меньшим числом зубьев называть шестернёй, а большое — колесом. Однако часто все зубчатые колёса называют шестерня́ми.

Работа цилиндрической зубчатой передачи

Зубчатые колёса обычно используются па́рами с разным числом зубьев с целью преобразования вращающего момента и числа оборотов валов на входе и выходе. Колесо, к которому вращающий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым. Если диаметр ведущего колеса меньше, то вращающий момент ведомого колеса увеличивается за счёт пропорционального уменьшения скорости вращения, и наоборот. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение — механическая мощность — останется неизменным. Данное соотношение справедливо лишь для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.

Билет 12

Начальными окружностями сопряженной пары зубчатых колес называются соприкасающиеся окружности, описанные из центров колес и катящиеся одна по другой без скольжения.

Основной окружностью называется окружность, разверткой которой является звольвентная профильная линия зуба в сечении, перпендикулярном к оси зубчатого колеса.

Делительной окружностью называется окружность, описанная из центра колеса, на которой шаг и угол зацепления изделия в торцевом сечении равны теоретическому шагу и углу зацепления режущего инструмента.

Начальная окружность в период нарезания называется делительной окружностью. У нормальных зацеплений начальная окружность совпадает с делительной.

Билет №5

Передаточное число. Это отношение числа зубьев колеса к числу

зубьев шестерни

В понижающих передачах передаточное число совпадает с передаточным отношением, по модулю равным отношению

угловых скоростей зубчатых колес.

Фактически, исходя из смысла определения, цифровое значение передаточного числа показывает однозначно лишь следующие факты: во сколько раз различаются линейные размеры (радиус, диаметр, длина окружности) обоих зубчатых колёс; на какую величину данная зубчатая передача может изменять две составляющие вращательного движения – крутящий момент и частоту вращения. При этом нет никаких указаний на то, с какого на какой из двух элементов зубчатой передачи должное передаваться вращение. Согласно тому же ГОСТу «шестерня» не обязательно является ведущим элементом^[5], а «колесо» не обязательно ведомым^[6]. Подстрочное примечание к определению терминов «колесо» и «шестерня» указывает лишь один случай однозначного соответствия – ведущий элемент может называться «шестернёй» лишь при равном числе зубьев с ведомым.

Введение в оборот термина «передаточное число» ГОСТом 16530-83 не очень понятно: в некотором смысле этот термин дублирует интернациональный термин «передаточное отношение»^[7]. Факт того, что большинство зубчатых передач в различных агрегатах имеют передаточное отношение больше единицы, привёл к тому, что зачастую в обиходе термины «передаточное отношение» и «передаточное число» воспринимаются как синонимы. Но на самом деле это ошибка. Учитывая особенности формулировки термина «передаточное число», следует всегда понимать, что передаточное число не обязательно равно передаточному отношению. Оно может совпадать с модулем его значения, если таковое больше единицы (ведущая шестерня меньше ведомой): ( ) если ( ) Или быть равным его обратному значению, если таковое меньше единицы (ведущая шестерня больше ведомой): ( ) если ( ) Единственным объяснением может быть лишь факт того, что формально передаточное отношение рассчитывается на основе угловых скоростей элементов зубчатой передачи и, таким образом, всегда будет являться иррациональным числом^[8]. Передаточное число всегда есть рациональное число и может быть легко определено простым действием деления, а полученный результат через его прямое или обратное значение может быть корректно использован в дальнейших расчётах.