Вопрос 23
Расстояние между осями зубчатых колес цилиндрической передачи по межосевой линии называется межосевым расстоянием:
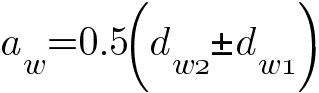
где dw1 и dw2 — начальные диаметры шестерни и колеса; знак плюс относится к передаче с внешним зацеплением, а минус — к передаче с внутренним зацеплением.
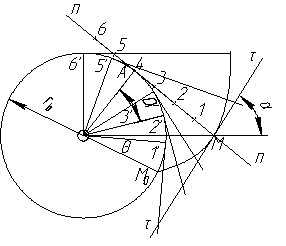
Угол зацепления w – это угол между линией зацепления и общей касательной к начальным окружностям, проведённой через полюс зацепления.
Угол зацепления
Угол зацепления определяется по таблице инволют. Инволюта угла зацепления определяется по формуле:
по таблице инволют определяем угол зацепления
Радиусы начальных окружностей
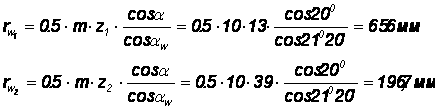
Межосевое расстояние
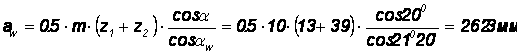
Вопрос24
Толщина зуба по дуге делительной окружности
При нулевом смещении толщина зуба равна половине шага по делительной окружности
.
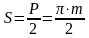При смещении исходного контура на величину x·m(рис. 29) толщина зуба вычисляется по формуле
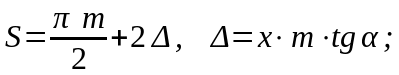
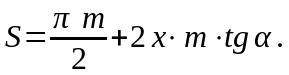
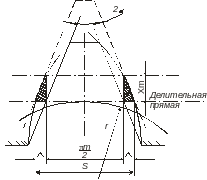
Вопрос 10
Эвольвента и ее св-ва.
Эвольвентой
круга называют кривую, которая описывает
любую точку прямой, перекатывающейся
без скольжения по окружности. При этом
прямую обычно называют производящей,
а окружность - основной 
.
Пусть
производящая прямая (рис. 2.36) n – n показана
в положении, когда она касается основной
окружности в точке А и требуется построить
эвольвенту, описываемую т. М. Делим
отрезок AM на равные части и откладываем
на
дуги
равные соответствующим частям отрезка
AM: 
и
так далее. Через полученные точки
проводим касательные и откладываем на
них отрезки, последовательно уменьшая
длину каждого отрезка на одну часть.
Соединяя концы отложенных отрезков,
получаем эвольвенту. Уравнение эвольвенты
получим из условия перекатывания
производящей прямой по
|
|
(2.45) |
|
Рис. 2.36 |
Обозначим
через 
острый
угол между касательной 
к
эвольвенте и радиус-вектором эвольвенты
ОМ. Этот угол называется углом профиля.
Угол, образованный начальным радиус-вектором
эвольвенты 
и
её текущим радиусом ОМ называется
эвольвентным углом (
).
Тогда условие (2.45) принимает вид: 
или 
.
Функция 
называется
инвалютой и обозначается "inv", то
есть уравнение может быть записано 
.
Радиус-вектор эвольвенты находится из
треугольника ОАМ
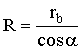
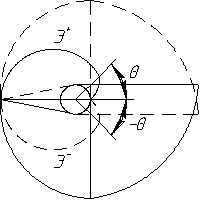
Эвольвента
имеет две ветви (рис. 2.37): положительная
ветвь 
получается
при перекатывании прямой против хода
часовой стрелки, отрицательная 
-
при перекатывании по ходу часовой
стрелки.
|
Рис. 2.37 |
Основные свойства эвольвенты
1.
Каждая ветвь эвольвенты вполне
определяется радиусом основной
окружности
и
начальной точкой 
.
2. Эвольвента не имеет точек внутри основной окружности.
3. Нормаль к любой точке эвольвенты направлена по касательной к основной окружности.
4. Центр кривизны эвольвенты лежит в точке касания нормали с основной окружностью .
. Основная теорема зацепления (теорема Виллиса)
Для
постоянства передаточного отношения
при зацеплении двух профилей зубьев
необходимо, чтобы радиусы начальных
окружностей зубчатых колёс, перекатывающихся
друг по другу без скольжения, оставались
неизменными. Если рассмотреть обращённое
движение начальных окружностей, когда
всей системе задана угловая скорость
(
),
то второе колесо будет условно неподвижным
иточка Р является
мгновенным центром относительного
вращения колёс (рис. 70,а). Эта
точка, называемая полюсом
зацепления,
где контактируют начальные окружности,
делит межцентровое расстояние на
отрезки, обратно пропорциональные
угловым скоростям, т. к.
.
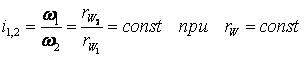Рассмотрим обращённое движение профилей зубьев зубчатых колёс (рис. 70, б).
рис. 70
Точка
контакта зубьев (точка к),
принадлежащая первому колесу, вращается
вокруг точки Р, которая будет мгновенным
центром скоростей. Скорость 
и
совпадает с общей касательной к профилям
в точке к при
условии постоянства этого контакта.
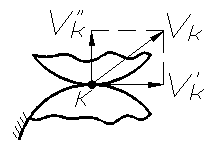В
противном случае постоянного контакта
не будет, так как появится составляющая 
и
профили разомкнутся (рис. 71). Так как
рассматривается произвольное положение
зубьев, то можно сформулировать теорему.
Нормаль NN к касающимся профилям зубьев, проведённая через точку их касания, делит межцентровое расстояние на части, обратно пропорциональные угловым скоростям.
Эта теорема, сформулированная Виллисом в 1841 г., определяет основной закон зацепления профилей, которые не могут быть произвольными, а должны быть специально подобраны.