4.1. Связь между дирекционными углами предыдущей и последующей линий

Задача заключается в том, чтобы по известному дирекцион-ному углу _1-2 стороны 1-2 вычислить дирекционный угол _2-3 стороны 2-3, если известен ^П₂, или ^Л₂ (правый или левый) угол между ними.

Х

Х

Х

Х

1

3

1

3

3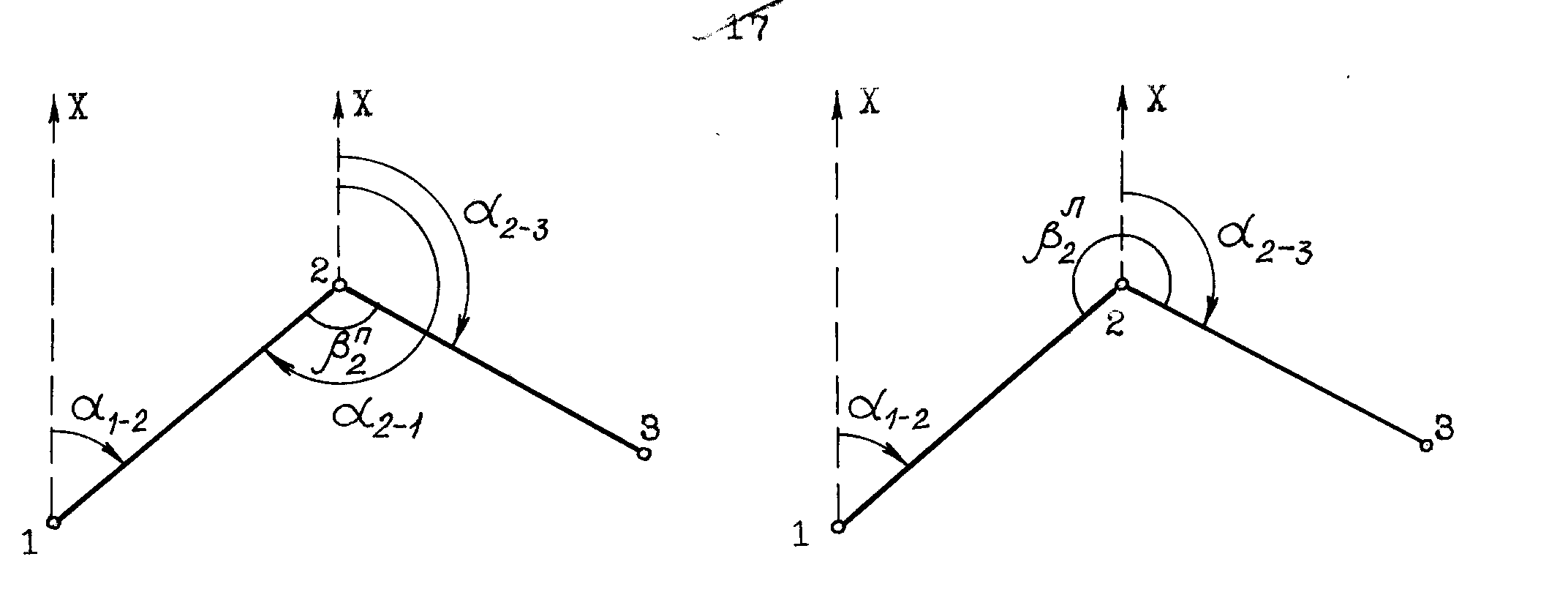

_2-3 = _2-1 - ^П₂ = _1-2 +180⁰ - ^П₂ , но ^П₂ = 360⁰- ^Л₂ ,

следовательно: _2-3 = _1-2 +180⁰- (360⁰ - ^Л₂) = _1-2 + ^Л₂ - 180⁰.

В общем виде можно записать :

_i+1 = _i + 180⁰ - ^П = _i + ^Л - 180⁰ .

Дирекционный угол последующей линии равен дирек-ционному углу предыдущей линии плюс 180⁰ и минус правый ^П по ходу угол между линиями (или плюс левый ^Л по ходу угол меж-ду линиями и минус 180⁰).

Если при вычислениях дирекционный угол получился больше 360⁰, то из него следует вычесть 360⁰.

По известным дирекционным углам предыдущей и последую-щей линий можно вычислить правый или левый углы между линиями:

^П = _i + 180⁰ - _i+1 или ^Л = _i+1 + 180⁰ - _i .

Правый по ходу угол между двумя линиями равен дирек-ционному углу предыдущей линии плюс 180⁰ и минус дирекционный угол последующей линии.

Левый по ходу угол между линиями равен дирекционному углу последующей линии плюс 180⁰ и минус дирекционный угол предыдущей линии.

4.2. Прямая геодезическая задача

По координатам начальной точки линии 1 вычислить коорди-наты конечной точки линии 2, зная ее направление _1-2 и длину d_1-2 .

Дано: Х₁, У₁, _1-2 , d_1-2 .

Найти: Х₂, У₂.

Из решения прямоугольного треугольника вычисляем приращения координат х_1-2 и у_1-2 :

X X х_1-2 = d_1-2 cosr_1-2 ,

у_1-2 = d_1-2 sinr_1-2 .

+y_1-2 2

r_2-3 d_2-3

+x_1-2

-x_2-3

d_1-2 3

r_1-2 +y_2-3

1 d_3-4

4

Координата конечной точки линии равна координате начальной точки этой линии плюс или минус соответствующее приращение координат между этими точками:

Х₂ = X₁ + Х_1-2 , У₂ = У₁ +У_1-2 .

Теперь, зная координаты точки 2, можно вычислить координа-ты точки 3, если известен дирекционный угол _2-3 и длина линии d_2-3 и т.д.

Как видно из рисунков, знаки приращений координат зависят от названия румба, поскольку эти приращения равны произведению горизонтального проложения на косинус или синус румба данной линии. По этим формулам всегда получим положительные величины, так как румб - острый угол. Поэтому для определения знаков приращений координат всегда надо учитывать название румба.

Х

+у_1-2 2

+х_1-2 -х_2-3

-у_4-1

1 + у_2-3 3

+х_4-1 -х_3-4

О 4 -y_3-4 У

При вычислении приращений координат на микро-калькуляторе можно вместо румбов использовать дирекционные углы, тогда знаки приращений будем получать автоматически.