П.2. Операторный метод

Рассчитаем начальные условия для переменных:

, .

Эти величины используются при написании уравнений цепи в операторной форме. Согласно законам Кирхгоффа (Рис. П.76) запишем следующую систему уравнений в операторной форме:

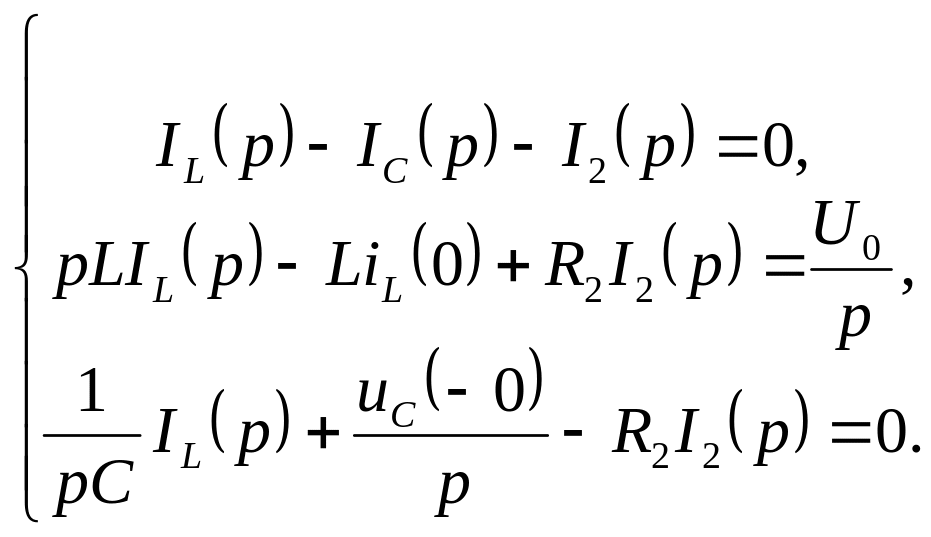
Подставим численные значения в данную систему

Приведем систему к операторному уравнению относительно операторного тока и сравним с ранее полученным решением

,

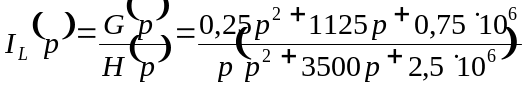где G(p) – полином числителя и H(p) – полином знаменателя.

Рекомендуется проверить правильность полученного уравнения с помощью пределов:

.

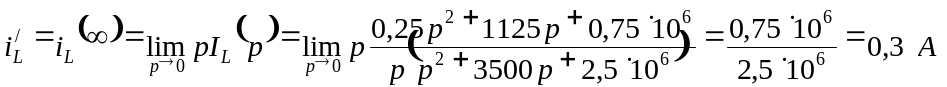Рассчитанные токи и совпадают с соответствующими токами, полученными по классическому методу.

Чтобы рассчитать ток будем использовать теорему разложения:

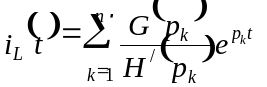_. (П.8)

1. Найдем корни from the equation H(p)=0

.

, , .

2. Произведем дифференцирование

.

3. Рассчитаем коэффициент для корня :

4. Рассчитаем коэффициент для корня :

5. Рассчитаем коэффициент для корня :

6. Используя (П.8) получаем формулу для тока:

A.

Эта формула совпадает с выражением (П.7) для , полученного классическим методом. Токи в других ветвях получают по аналогии.

П.3. Метод переменных состояния

При составлении уравнений состояния с помощью законов Кирхгофа для уменьшения промежуточных преобразований рекомендуется для индуктивности использовать переменные и (для напряжения), для емкости - и (для тока). Следует также уравнения по возможности записывать так, чтобы в каждое из них входило не более одной производной от переменной состояния. После составления уравнений по законам Кирхгоффа из них исключают все алгебраические переменные, т.е. переменные, не являющиеся переменными состояния.

Соблюдая сказанное, непосредственно по схеме запишем систему уравнений:

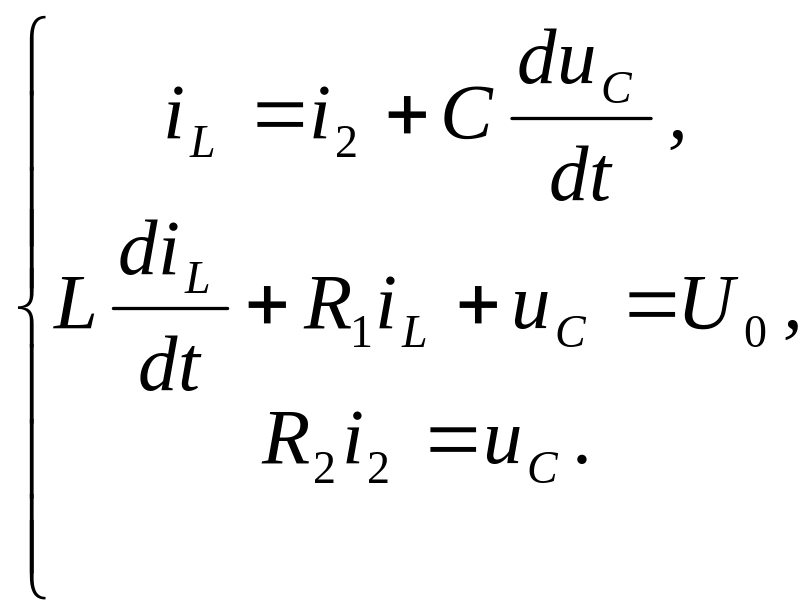
Здесь - алгебраическая переменная. После ее исключения получаем систему в виде:

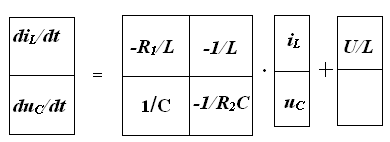(П.9)

После подстановки численных значений параметров элементов цепи система (П.9) принимает вид

,

при

.

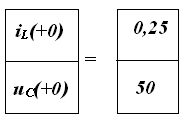Корни характеристического уравнения совпадают с ранее найденными значениями:

Система дифференциальных уравнений решается различными методами численного интегрирования. Интервал интегрирования определяется следующим образом

Если для интегрирования используется явный метод Эйлера, то шаг интегрирования можно принять равным значению . В общем случае шаг , где - одна из норм матрицы A. Общее число шагов интегрирования равно

Можно видеть, что N пропорционально числу обусловленности матрицы A и может оказаться весьма большим для жестких систем.

Приложение 4

Расчет переходного процесса с помощью интеграла Дюамеля

Пример.

Найти и при включении ключа в цепи на рис. П.3.1. Напряжение источника , , , , .

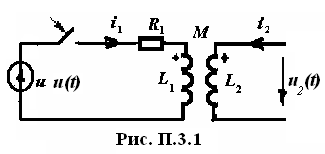
Решение

Переходная проводимость цепи, состоящей из последовательно включенных и , равна

,

где ,

.

Первое слагаемое в формуле (4.6) отсутствует, так как .

Учитывая, что

,

получим выражения для тока в первичной обмотке:

.

При интегрировании учитываем, что от не зависит

.

Напряжение на зажимах вторичной обмотки:

.

ЛИТЕРАТУРА

Основная

1. Нейман Л.Р., Демирчян К.С. ТОЭ. - Л.: Энергоиздат, 1981. - Т. 1,2.

2. Теоретические основы электротехники. Под ред. П.А. Ионкина. Т. 1,2. - М.: ВШ., 1976.

3. Теоретические основы электротехники. Под ред. Г.И. Атабекова. Т. 1,2 - М.: Энергия, 1979.

4. Сборник задач и упражнений по ТОЭ. Под ред. П.А. Ионкина. - М.: Энергоиздат, 1982. - 766с.

5. Пашенцев И.Д. Методические пособия по решению задач курса ТОЭ. - Л.: ЛИИЖТ, 1981. - Ч. I-VI.

6. Бессонов Л.А. Сборник задач по ТОЭ. - М.: ВШ, 1988.

7. Бессонов Л.А. Теоретические основы электротехники. - М.: ВШ, 1978. - Т.1,2.

8. Новгородцев А.Б. 30 лекций по теории электрических цепей. - СПб.: Политехника, 1995. - 519с.

9. Шимони К. Теоретическая электротехника. - М.: МИР, 1964. - .773с.

10. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. - М.: Энергоиздат, 1989. - 333с.

11. Белецкий А.Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986. - 554с.

12. Поливанов К.М. Теоретические основы электротехники. - М.: Энергия, 1975. - Т.3. - 352с.

13. Ким К.К. Самоучитель по теории линейных электрических цепей- СПб.: ПГУПС, 2005. - Ч. 1, 2, 3, 4.

14. Литература информационно-методического обеспечения учебного процесса, разработанная кафедрой ТОЭ.

Дополнительная

1. Матханов П.Н. Основы анализа электрических цепей. - М.: ВШ, 1990

2. Практикум по ТОЭ. Под ред. Шакирова М.А. - СПб.: СПбГТУ, 1995. - Ч. 1, 2, 3.

3. Шебес М.Р. Задачник про теории линейных электрических цепей. - М.:ВШ, 1973. - 655с.

4. Демирчян К.С., Бутырин П.Л. Моделирование и машинный расчет электрических цепей. - М.: ВШ, 1988.

5. Кухаркин Е.С. Основы технической электродинамики. - М.: ВШ, 1969 - Ч. 1, 2.

Рекомендуется использование пакетов программ Pspice, Workbench, Matlab, Mathcad, Elcat.

40