Примеры расчетов переходных процессов классическим методом в контурах I порядка
Пример 1.
Рассчитать
переходный процесс в цепи, показанной
на рис. П1.1: вывести закон изменения тока
в индуктивности и построить график
зависимости
.
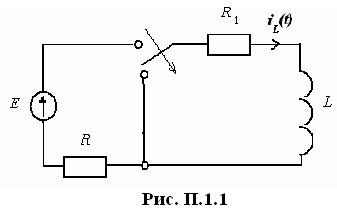
Параметры элементов
цепи:
.
Решение
1.
- момент коммутации.
2. В качестве искомой
переменной выбираем
,
т.к. этот ток подчиняется законам
коммутации.
2. Для послекоммутационного
режима
по законам Кирхгофа составим уравнения
цепи:
.
3. Решение ищем в виде
.
(П.1.1)
4. Составим характеристическое уравнение и найдем его корень:
Характер переходного процесса в цепи - апериодический.
5. Рассчитаем
до коммутации
:
.
6. Рассчитаем
в новом установившемся режиме
:
,
т. к. вся энергия
уйдет на нагрев резистора
.
7. Запишем уравнение (П.1.1) для момента коммутации:
,
затем найдем
постоянную интегрирования:
8. Формируем выражение тока:
.
Найдем напряжение
на индуктивности:
.
Построение графика тока:
Определим постоянную
времени переходного процесса
.
Длительность
переходного процесса: равна
.
Составим таблицу для построения графика
-
t
0
0,1t
0,25t
0,5t
0,75t
t
1,5t
2t
3t
4t
5t
5
4,52
3,89
3,03
2,36
1,84
1,12
0,68
0,25
0,09
0
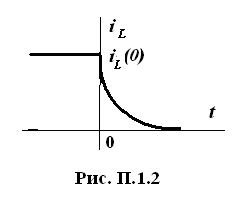
По точкам строим график, качественно он показан на рис. П.1.2.
Пример 2.
Рассчитать
переходный процесс в цепи, показанной
на рис. П.1.3: вывести закон изменения
напряжения на конденсаторе и тока
,
построить графики.
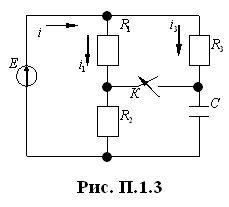
Параметры элементов
цепи:
;
;
;
.
Решение
1. - момент коммутации.
2. В качестве искомой
переменной выбираем
,
т.к. это напряжение подчиняется законам
коммутации.
2. Для послекоммутационного режима составим уравнения цепи:
И запишем формулу
для тока:
.
Из третьего уравнения полученной системы дифференциальных уравнений имеем:
.
3. Решение ищем в виде
.
(П.1.2)
4. Составим характеристическое уравнение и найдем его корень:
Характер переходного процесса в цепи - апериодический.
5. Рассчитаем
до коммутации
:
,
,
,
т.к.
,
6. Рассчитаем в новом установившемся режиме :
,
т.к. сопротивление конденсатора
постоянному току
и падением напряжения на
можно пренебречь.
7. Запишем уравнение (П.1.2) для момента коммутации:
,
подставим численные значения и найдем постоянную интегрирования:
.
8. Формируем выражение для напряжения на конденсаторе:
.
Найдем выражение для тока:
:
.
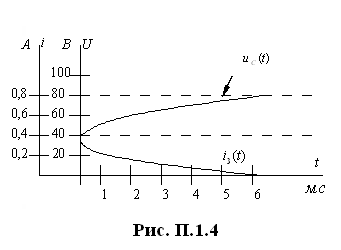
Построение графика напряжения на конденсаторе и тока :
Определим постоянную
времени переходного процесса
.
Длительность переходного процесса:
Использую полученные формулы и задаваясь моментами времени, по точкам строим необходимые графики (рис. П.1.4).
Пример 3.
Рассчитать операторным методом переходный процесс в цепи, показанной на рис. П.1.1: вывести выражения для токов.
Параметры элементов
цепи:
.
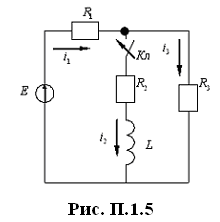
Решение
1. - момент коммутации.
2. В качестве искомой
переменной выбираем
,
т.к. этот ток подчиняется законам
коммутации.
2. Для послекоммутационного режима по законам Кирхгофа составим уравнения цепи:
(П.1.3)
Осуществим преобразование системы с целью получения одного дифференциального уравнения. Это целесообразно сделать относительно искомой величины на энергоемком элементе .
После математических преобразований имеем:
3. Решение ищем в виде
.
(П.1.4)
4. Составим характеристическое уравнение и найдем его корень:
Характер переходного процесса в цепи - апериодический.
5. Рассчитаем до коммутации :
.
6. Рассчитаем в новом установившемся режиме :
7. Запишем уравнение (П.1.4) для момента коммутации:
,
затем найдем
постоянную интегрирования:
8. Формируем выражение тока:
.
Остальные токи находим из системы уравнений (П.1.3), опускаем промежуточные выкладки и получаем:
и
.
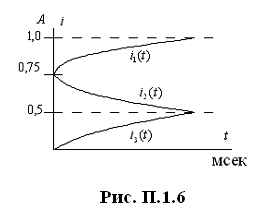
Построение графиков токов:
Определим постоянную
времени переходного процесса
.
Длительность переходного процесса: равна .
По точкам строим график, качественно он показан на рис. П.1.6.
Приложение 2