V. Особенности расчета переходных процессов в цепях с емкостными контурами и индуктивными сечениями

Контуры, состоящие только из емкостей или емкостей и источников ЭДС, называются емкостными контурами.

Сечения, состоящие только из индуктивностей или индуктивностей и источников тока, называют индуктивными сечениями.

Если в цепи в результате коммутации образуются емкостные контуры или индуктивные сечения или те и другие, то законы коммутации применимы только к емкостям и индуктивностям, не входящим в указанные контуры и сечения. Для емкостей емкостных контуров применяется закон неизменности заряда, а для индуктивностей индуктивных сечений применяется закон неизменности потокосцепления. Рассмотрим эти законы.

Закон неизменности заряда формулируется следующим образом: алгебраическая сумма зарядов емкостей, присоединенных к любому общему узлу, неизменна в момент коммутации. Т.е. , отсюда

. (5.1)

Сумму зарядов записывают с учетом положительных направлений напряжений на емкостях аналогично I закону Кирхгофа для токов, при этом учитывают только емкости емкостных контуров.

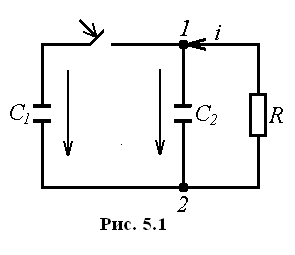
Пример (рис. 5.1).

Полагаем, что предварительно заряжен до напряжения , т.е. а

В емкостном контуре имеем два узла 1 и 2. Для любого из этих узлов закон (5.1) принимает вид:

но поэтому

После коммутации цепь описывается уравнением , но Учитывая это, получим Решение этого уравнения записывается следующим образом , где

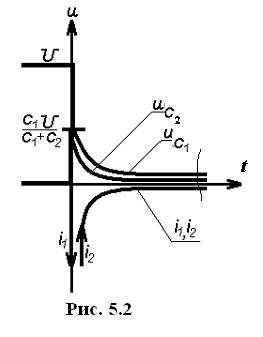
Скачкообразное изменение напряжений обусловлено импульсными токами емкостей, которые возникают в момент коммутации и осуществляют мгновенное перераспределение зарядов между емкостями (рис. 5.2).

Закон неизменности потокосцепления формулируется так: алгебраическая сумма потокосцеплений индуктивностей в любом замкнутом контуре не изменяется во время коммутации, т.е.

или .

Сумму записывают с учетом положительных направлений токов в индуктивностях и направления обхода контура аналогично II закону Кирхгофа для напряжений, при этом учитываются только индуктивности индуктивных сечений.

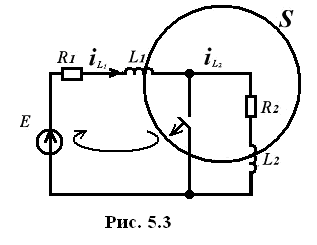
Пример.

После коммутации цепи (рис. 5.3) имеем один контур, в который входят обе индуктивности сечения s.

Можно записать где

поэтому

После коммутации цепь описывается уравнением:

Решение этого уравнения следующее: где .

П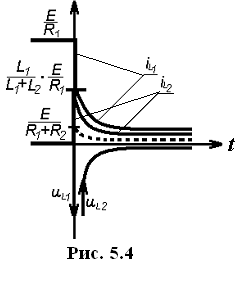 ереходной ток равен: .

В момент коммутации токи изменяются скачком (рис. 5.4), т.к. на индуктивностях возникают импульсные напряжения, приводящие к мгновенным перераспределениям магнитного потока между катушками.

Пример

Необходимо составить уравнения для определения начальных значений напряжений на емкостях схемы (рис. 5.5).

После замыкания ключа в схеме образуется емкостной контур . Для узлов 1 и 2 составим уравнения неизменности заряда:

По II закону Кирхгофа для емкостного контура получим уравнение:

Из этих уравнений определим при известных значениях .

Емкость не входит в емкостной контур, поэтому ее напряжение непрерывно:

Пример

С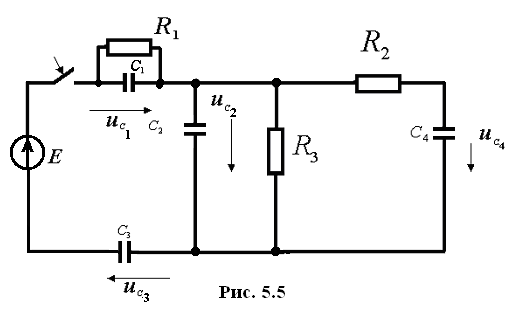 оставить уравнения для определения начальных значений токов в индуктивностях схемы (рис. 5.6).

При отключении ключа в схеме образуется индуктивное сечение .

Для указанных на рис. 5.6 трех контуров составим уравнения неизменности потокосцеплений:

По I закону Кирхгофа для сечения получим уравнение:

Из этих уравнений находим

Индуктивность в сечение не входит, поэтому