ПЕТЕРБУРГСКИЙ

Г ОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

K.K. Kим

САМОУЧИТЕЛЬ ПО ТЕОРИИ ЛИНЕЙНЫХ

ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Часть 5 Учебное пособие

Санкт-Петербург

2005

УДК 621.3.01

ББК 31.211

Kим K.K.

Самоучитель по теории линейных электрических цепей. Ч.4: Учебное пособие. – СПб.: Петербургский государственный университет путей сообщения, 2005. – 60 с.

Библ.: 20. Рис. 106.

Основные проблемы теории и расчета переходных процессов в линейных электрических цепях рассмотрены в данном пособии.

Учебное пособие написано в соответствии с дисциплиной «Теоретические основы электротехники». Пособие предназначено для студентов-заочников электромеханических и электротехнических специальностей.

Пособие может быть полезно инженерам и аспирантам.

 K.K. Kим, 2005

СОДЕРЖАНИЕ

		с
IV 4.1 4.2 4.3 V	Расчет переходных процессов в линейных цепях при воздействии ЭДС произвольной формы Метод вариации произвольных постоянных Интеграл Дюамеля Переходной ток при воздействии импульсной ЭДС Особенности расчета переходных процессов в цепях с емкостными контурами и индуктивными сечениями Заключение Приложение 1 Приложение 2 Приложение 3 Приложение 4 Литература	4 4 7 10 15 20 25 33 39 58 59

IV. Расчет переходных процессов в линейных цепях при воздействии эдс произвольной формы

До этого времени рассматривались переходные процессы, когда напряжения или ЭДС, действующие в цепи, были либо постоянными, либо изменялись во времени по закону синуса. Поскольку цепи предполагались линейными, то вид установившихся токов был ясен заранее, эти токи по виду совпадали с напряжением или ЭДС.

Рассмотрим вопросы расчета переходных процессов в общем случае, когда в цепи действует ЭДС произвольной формы. Наиболее общий метод расчета переходных процессов в подобных случаях – метод вариации произвольных постоянных.

4.1. Метод вариации произвольных постоянных

Допустим, что уравнения переходных процессов в некоторой линейной цепи после исключения всех искомых переменных (токов), за исключением одной, сведены к одному уравнению:

,

где  функция, определяемая ЭДС, действующими в цепи и имеющими произвольный характер.

Как и обычно находим решение однородного уравнения, соответствующего исходному уравнению. Пусть это решение имеет вид (штрихи для свободного тока не пишем, чтобы не путать со знаком производной)

, (4.1)

где  корни характеристического уравнения (простые числа), которое выглядит следующим образом:

.

Идея метода состоит в том, что в уравнении (4.1) рассматриваются не как постоянные, а как переменные, которые следует найти с учетом правой части исходного уравнения.

Поступают следующим образом. Составим уравнения:

(4.2)

Штрих над означает производную.

Подставив уравнение (4.1) в исходное уравнение после приведения подобных членов, получим уравнение:

(4.3)

Т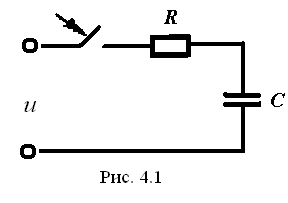 аким образом, для величин получена система линейных уравнений (4.2), (4.3) из уравнений. Решая ее, находим эти постоянные, а затем квадратурами находим сами величины в зависимости от и произвольных постоянных . Последние определяем из начальных условий, а те в свою очередь – с помощью законов коммутации.

Пример.

Пусть имеется цепь из последовательно соединенных (рис. 4.1). Она включается на напряжение . Коммутация происходит при нулевых начальных условиях .

Запишем уравнение цепи .

Решение однородного уравнения равно

. (4.4)

Рассмотрим как функцию времени. Поэтому

.

Подставим эту формулу и уравнение (4.4) в исходное уравнение:

, .

,

.

Данное выражение подставляем в уравнение (4.4):

. (4.5)

При имеем

, .

Значение вносим в уравнение (4.5) и находим напряжение на конденсаторе:

.

Найдем выражение для тока:

.