12. Расчет переходных процессов в нелинейных цепях

Переходные процессы в нелинейных электрических цепях описываются нелинейными дифференциальными уравнениями. Для решения этих уравнений нет регулярных методов. Если иметь в виду аналитическое решение, то, как правило, каждое нелинейное дифференциальное уравнение требует особого подхода, однако существуют приближенные методы, носящие более или менее общий характер. К ним относятся графические методы и приближенные аналитические методы (метод кусочно-линейной аппроксимации, метод последовательных интервалов). Рассмотрим их.

В последнее время широкое применение находит компьютерная техника, использование которой позволяет значительно повысить эффективность ниже рассматриваемых расчетных методов.

12.1. Графический метод расчета переходных процессов

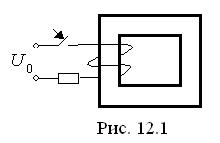
Рассмотрим данный метод на примере расчета процесса включения катушки с ферромагнитным сердечником на постоянное напряжение ( ) (рис. 12.1).

Дифференциальное уравнение, которое описывает процесс включения, выглядит следующим образом:

, (12.1)

г

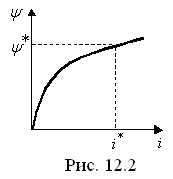
де - активное сопротивление обмотки катушки, Зависимость нелинейна из-за насыщения сердечника (рис. 12.2).

Допустим, что перед включением сердечник был размагничен. В таком случае зависимость будет характеризоваться начальной кривой намагничивания. Необходимо решить уравнение (12.1) при , представленной на рис. 12.2.

Запишем уравнение (12.1) в виде (разделим переменные):

. (12.2)

Пользуясь зависимостью, строим кривую .

Для этого, задаваясь последовательностью значений i для каждого из них, вычисляем и определяем соответственно этому значению тока по кривой (рис. 12.2). В результате получим некоторую кривую (рис. 12.3). Тогда время, соответствующее значению , будет равно заштрихованной площади на рис., согласно формуле (12.2).

В результате получим кривую (кривая 1 на рис.). Если теперь по этой кривой для каждого значения потокосцепления ( ) найти соответствующий ему ток из графика , то можно построить зависимость тока от времени ( ) (кривая 2 на рис. 12.4).

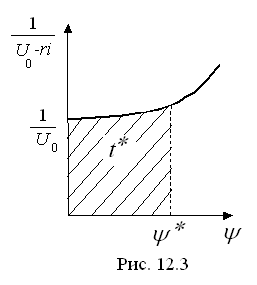
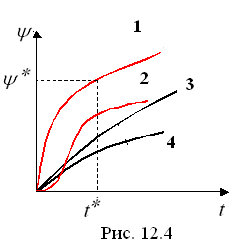
На рис. 12.4 показаны кривые (кривая 3) и (кривая 4), если бы зависимость между и i была бы линейной и совпала с начальной частью кривой . Видно, что при насыщении растет значительно быстрее, чем в линейном случае. В линейном случае уравнение (12.1) получает вид:

,

где L находится по прямолинейной части характеристики .

12.2. Метод последовательных интервалов (метод Эйлера)

Метод последовательных интервалов представляет собой метод численного интегрирования дифференциального уравнения первого порядка.

Интервал времени “S”, в течение которого рассматривается переходный процесс, делится на N равных частей. Расстояние между соседними точками называется шагом сетки, а точки - узлами сетки. Производные заменяются конечными разностями, и расчет производится точно также как и в методе конечных разностей.

Рассмотрим процесс включения катушки с ферромагнитным сердечником на постоянное напряжение. Запишем уравнение цепи

. (12.3)

Считаем, что зависимость задана (рис. 12.2).

Вводим расчетную сетку с шагом h.

, тогда уравнение (12.3) представимо следующим образом: или

. (12.4)

Пусть , при - нулевые начальные условия.

При имеем согласно формуле (12.4) , зная , по характеристике находим .

При , по находим и т.д.