11.7. Феррорезонанс при параллельном соединении катушки с ферромагнитным сердечником и конденсатора

П ренебрежем потерями в цепи (рис. 11.11) и высшими гармониками. Тогда токи и будут в противофазе. Ток I будет равен абсолютному значению разности токов и , т.е. .

- характеристика катушки, - характеристика конденсатора (рис. 11.12).

В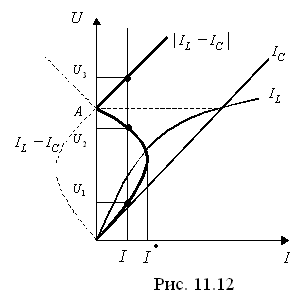 ычтем графически из характеристики характеристику и получим характеристику .

Напряжение, при котором ток во внешней цепи равен заданному

т

U

оку I , определим, находя точки пересечения зависимости с прямой I=const.

Если , то таких точек может быть три. Точки для и соответствуют преобладанию в цепи емкости, точка для - преобладанию индуктивности. Точка А является точкой резонанса, т.к. токи и взаимно компенсируются.

В рассматриваемом случае резонанса, в отличие от линейных цепей с постоянными параметрами, можно достичь изменением внешнего приложенного напряжения. Это явление также относится к явлению феррорезонанса, а конкретно, к феррорезонансу в параллельной цепи.

В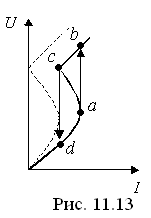 следствие наличия потерь и высших гармоник, фактическая характеристика приобретет вид (сплошная кривая), показанный на рис. 11.13

При плавном увеличении тока в цепи будут происходить срывы. Часть характеристики ас соответствует неустойчивому режиму.

Найдем выражения для максимального напряжения при данном виде феррорезонанса. Предположим, что цепь на рис. 11.11 запитывается напряжением Найдем ток, протекающий через катушку, учитывая ее нелинейную характеристику:

Учтем только основную гармонику тока

.

Найдем ток через конденсатор .

Выражение для тока в общей ветви найдем (при резонансе ток равен нулю), используя I закон Кирхгофа

.

отсюда получим . Из полученного выражения найдем

.

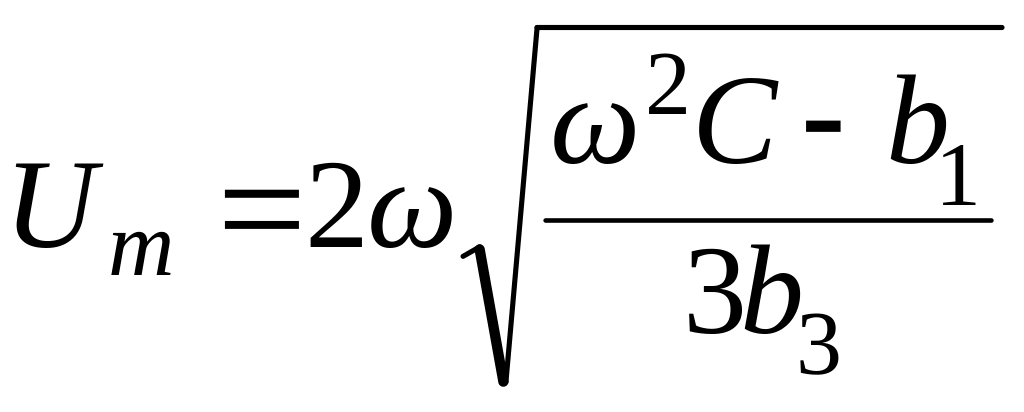11. 8. Управляемые индуктивные элементы. Ферромагнитный усилитель мощности

Д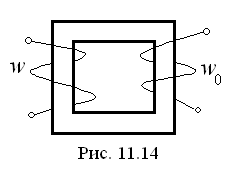 опустим, что имеется ферромагнитный сердечник с двумя обмотками. Основная обмотка имеет количество витков равное w, обмотка управления c количеством витков , питается от регулируемого источника постоянного тока. Процессы, происходящие в основной обмотке, определяются магнитным сопротивлением сердечника. Если сердечник не насыщен, то индуктивность L основной обмотки будет большой, а если насыщен, то малой. Таким образом, изменяя магнитное состояние сердечника, можно воздействовать на работу основной обмотки, например, регулировать ток в ней. Для этой цели используются обмотка управления с количеством витков . Регулируя МДС этой обмотки, т.е. ее ток, можно изменять магнитное состояние сердечника и тем самым изменять индуктивность основной обмотки. Таково рода устройства будем называть управляемыми индуктивными элементами.

Управляемые индукционные элементы могут быть использованы, например, для регулировки напряжения в ЛЭП или в качестве переменной индукционной нагрузки при испытаниях электрических машин.

Широкое распространение получили так называемые ферромагнитные усилители мощности, в которых используются управляемые нелинейные элементы.

Усилитель состоит из двух одинаковых ферромагнитных сердечников (рис. 11.15). На каждом сердечнике имеется две обмотки с числом витков и . Обмотки с числом витков (основные) включены последовательно с приемником, имеющим сопротивление R. Э та цепь питается от источника переменного напряжения u частоты f . Обмотки с числом витков составляют управляющую цепь. Пусть в управляющей цепи протекает постоянный ток . Чем больше , тем сильнее подмагничивание этим током сердечника и тем меньше индуктивное сопротивление переменному току со стороны обмоток и, соответственно, тем меньше будет напряжение на катушке при заданном токе I. На рис. 11.16 приведено семейство характеристик при разных значениях подмагничивающего тока .

Вводя в рассмотрение эквивалентные синусоиды и пренебрегая потерями в сердечниках и обмотках катушек, мы должны считать напряжения IR и сдвинутые на угол . В таком случае:

_.

П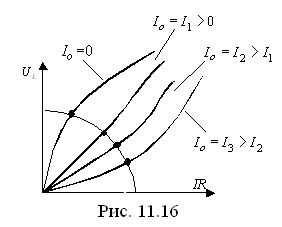 ри U=const это уравнение определяет окружность радиуса U с центром в начале координат. Точки пересечения окружности (рис. 11.16) с характеристиками дают возможность найти зависимость (рис. 11.17).

При условии имеем возможность управлять значением мощности в приемнике при незначительной мощности в управляющей цепи, т.е. получаем усилитель мощности.

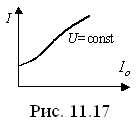В усилителе два одинаковых сердечника и обмотки навиты в таком направлении, чтобы в цепи приемника взаимно компенсировались четные гармоники, появляющиеся в результате подмагничивания сердечников током . При этом также компенсируются в управляющих обмотках ЭДС частоты f, вызываемым током I.