11.4. Уравнение и схема замещения катушки с ферромагнитным сердечником
Р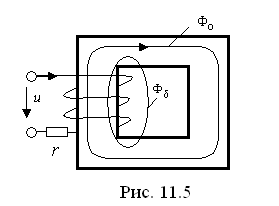
ассмотрим
катушку с ферромагнитным сердечником
с числом витков
(рис.) и активным сопротивлением обмотки
катушки
(рис. 11.5).
Магнитный поток, созданный током ( ), протекающим по обмотке катушки, можно разделить на два:
,
где
- рабочий магнитный поток,
- поток рассеяния.
Аналогично подобную операцию можно провести и с потокосцеплением:
,
здесь
- потокосцепление, нелинейно связанное
с током i;
а
- линейно связано с током i,
т.к.
=
const
(магнитный поток рассеяния в основном
замыкается по воздуху, у которого
).
Согласно II закону Кирхгофа, имеем
или
- это уравнение нелинейное, т.к. даже
если приложенное напряжение (u)
синусоидально, ток (i)
и напряжение (
)
- несинусоидальные. Используем метод
эквивалентных синусоид и заменим
и
синусоидальными величинами. Это позволит
перейти к комплексным величинам, имеем:
или
.
П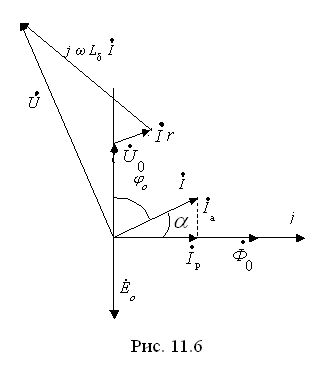
отери
в ферромагнитном сердечнике определяются
формулой
,
,
поэтому вектор тока
на диаграмме (рис. 11.6) по направлению не
совпадает с
.
Т.о. поток
не совпадает с током
из-за наличия потерь в сердечнике.
ЭДС,
обусловленная рабочим магнитным потоком,
равна
;
соответствующее напряжение
.
Ток
можно
разложить на составляющие
,
,
где
- реактивная составляющая;
- активная составляющая. Угол между
векторами тока и реактивной составляющей
(
)
называется углом потерь.
Соответственно схема замещения может быть представлена следующим образом (рис. 11.7).
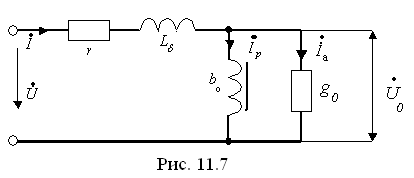
Реактивная
проводимость в схеме равна:
; а активная проводимость определяется
следующим образом:
.
Отсюда видно, что активная проводимость
пропорциональна мощности потерь в
ферромагнитном сердечнике. Определим
комплексную проводимость
,
где
- комплексное электрическое сопротивление.
11.5. Комплексное магнитное сопротивление
То
обстоятельство, что поток
в ферромагнитном сердечнике катушки
отстает по фазе на угол
от намагничивающего тока i
и, следовательно, от МДС «
»,
можно учесть вводом в закон магнитной
цепи комплексного магнитного сопротивления
сердечника:
.
При этом закон Ома для магнитной цепи пишется следующим образом:
,
где
,
l
– длина сердечника, S
– его поперечное сечение,
- комплексная магнитная проницаемость,
учитывающая и потери в сердечнике.
Существует важная связь между комплексным
магнитным сопротивлением и комплексным
электрическим сопротивлением
.
По
закону Ома имеем
.
Комплексная проводимость равна
.
Приравнивая действительные части, получим
.
Т.о.
пропорционально потерям в сердечнике.
Используя
понятие о комплексном магнитном
сопротивлении и, соответственно, о
комплексной магнитной проницаемости,
мы получаем возможность описывать
периодические процессы также и в
магнитных цепях с помощью комплексного
метода. Но
и
являются нелинейными функциями от МДС
или магнитного потока
.
,
.
1I.6. Феррорезонанс при последовательном соединении катушки с ферромагнитным сердечником и конденсатора
Условие
резонанса напряжений в линейной цепи
следующее:
,
резонансная частота равна
.
П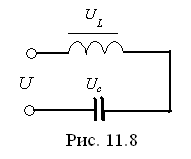
ри
резонансе
и резонансные характеристики:
совпадают, т.е. резонанс имеет место при
любом напряжении (
),
лишь бы выполнялось условие
.
Для случая нелинейной цепи ситуация
несколько изменяется.
Рассмотрим процессы, происходящие в нелинейной цепи, показанной на рис. 11.8.
Д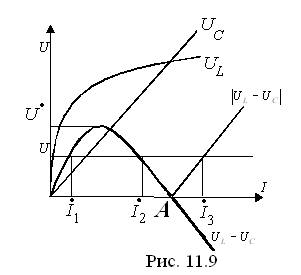
окажем,
что в цепи отсутствуют потери. Заменим
несинусоидальные кривые напряжения и
тока синусоидальными, выбрав их равными
первым гармоникам. При этих условиях
напряжения
и
по фазе прямо противоположны друг другу.
Напряжение
,
т.е. равно абсолютному значению разности
и
.
Допустим, что
- характеристика катушки,
- характеристика конденсатора известны
(рис. 11.9).
Вычитая
графически из зависимости
зависимость
,
получим
.
Видим, что при
возможны три точки пересечения
характеристики
с прямой U=const.
Точки
для
токов
,
соответствуют преобладанию индуктивности,
точка для
- преобладанию ёмкости.
Особая
точка А
является точкой резонанса, т.к. в этой
точке
и
взаимно компенсируются, т.о. в отличие
от линейных цепей, резонанса в
рассматриваемой цепи можно достичь
изменением приложенного напряжения U.
Это объясняется тем, что индуктивность
катушки с ферромагнитным сердечником
зависит от величины тока и, следовательно,
изменяется при изменении напряжения
на зажимах всей цепи. Это явление
называется явлением феррорезонанса. В
данном случае имеем дело с феррорезонансом
в последовательной цепи.
Вследствие
наличия в цепи потерь и высших гармоник,
фактическая характеристика приобретает
вид (сплошная кривая, рис. 11.10). П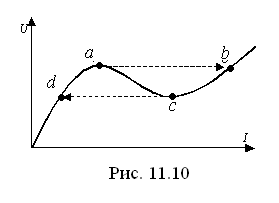
овышая
напряжение, дойдем до точки а,
далее произойдет срыв из точки a
в точку
b,
сопровождающийся
скачкообразным увеличением тока. При
дальнейшем увеличении напряжения ток
падает плавно. При понижении напряжения
ток плавно уменьшается до точки
с,
в которой
происходит срыв в точку
d,
который сопровождается
резким уменьшением тока. При этих срывах
происходит изменение угла сдвига фаз
в цепи (тока относительно приложенного
напряжения U).
При U=const падающая часть ac характеристики является областью неустойчивых режимов. Пусть при U=const некоторому режиму соответствует точка на участке ас. Тогда всякое случайное увеличение тока приведет к уменьшению падения напряжения в цепи, следовательно, к дальнейшему увеличению тока. Наоборот, всякое случайное уменьшение тока приведет к увеличению падения напряжения, следовательно, к дальнейшему уменьшению тока. В обоих случаях изменение тока будет продолжаться до тех пор, пока ток не достигнет значения, определенного точкой пересечения прямой U=const с одной из падающих частей характеристики. В любых режимах этих частей характеристики режим будет устойчив, т.к. случайное увеличение тока приведет к увеличению падения напряжения и ток должен будет уменьшиться, а случайное уменьшение тока приведет к уменьшению падения напряжения и ток должен будет увеличиться. Включив последовательно с цепью достаточно большое линейное сопротивление, можно получить устойчивую работу и на падающем участке характеристики.
Найдем
выражения для максимального тока при
данном виде феррорезонанса. Предположим,
что катушка имеет характеристику,
описываемую следующим выражением:
Также допустим, что по цепи протекает
синусоидальный ток
.
Возведем в третью степень и получим
.
Учтем
только основную гармонику в выражении
для напряжения на индуктивности:
.
Напряжение
на конденсаторе равно
.
Далее
найдем выражение для напряжения на
зажимах цепи (по условию резонанса оно
равно нулю)
.
Раскроем выражения членов данной суммы
Отсюда получаем
.
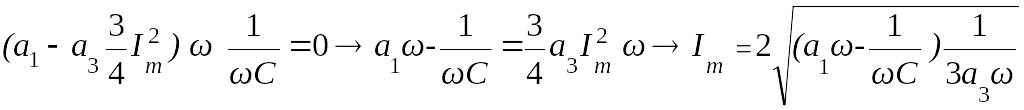