10.5. О расчёте постоянного магнита

П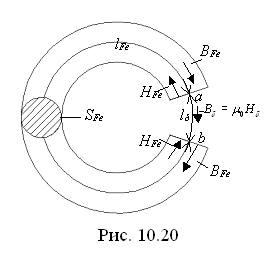 остоянный магнит представляет из себя кольцевой стальной сердечник с воздушным зазором (рис. 10.20). Предположим, что размеры сердечника l_Fe, S_Fe и кривая размагничивания. B(H) для его материала задана. Требуется определить магнитный поток в воздушном зазоре, если сердечник предварительно намагничен до насыщения.

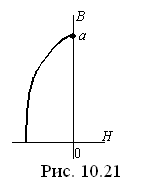
После намагничивания кольцевого сердечника без воздушного зазора магнитная индукция в нём равна B_r, напряжённость поля равна 0.На петле гистерезиса (часть кривой приведена на рис. 10.21) такое состояние соответствует верхней точке кривой размагничивания (точка а).

При наличии воздушного зазора напряжённость поля в сердечнике не равна 0. В самом деле, по закону полного тока имеем

. (10.1)

Если l_δ<<l_Fe, то можно считать S_δ=S_Fe. Поэтому

и из уравнения (10.1) следует

,

где - коэффициент размагничивания.

О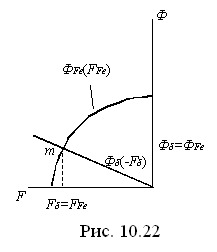 трицательное значение H_Fe означает, что при наличии зазора начальная индукция снижается по сравнению с это следует из выражения . Так как отрицательному значению H_Fe соответствует положительное значение B_Fe=B_δ, то магнитное состояние сердечника определяется одной из точек кривой размагничивания (второй квадрант петли гистерезиса на рис. 10.22)

Построим зависимость от МДС в сердечнике . Для этого умножим ординаты точек кривой размагничивания на S_Fe, а абсциссы умножим на l_Fe. Построим далее зависимость Ф_δ от МДС воздушного зазора F_δ.

.

Отсюда получаем выражение , которому соответствует прямая линия.

Так как , то магнитный поток определяется ординатой точки , а МДС абсциссой указанной точки.

XI. Нелинейные электрические и магнитные цепи при периодических процессах

11.1. Особенности периодических процессов в нелинейных цепях

Для исследования цепей переменного тока характеристики нелинейного элемента могут быть представлены различным образом. Характеристика резистивного нелинейного элемента задается в виде ВАХ u(i), i(u), либо с помощью дифференциального сопротивления “ ” или дифференциальной проводимости “ ” в зависимости от тока или напряжения ( ). Характеристика нелинейной индуктивности может быть, представлена в виде ψ(i) или в виде дифференциальной индуктивности , зависящей от тока или потокосцепления ( ). Аналогично представляется характеристика и для нелинейной емкости в виде зависимости q(u) или с помощью дифференциальной емкости “ ”, зависящей от напряжения или заряда ( ). При решении некоторых задач характеристики нелинейных элементов могут быть представлены в виде зависимостей для действующих значений.

Характер физических процессов в нелинейных цепях, когда эти процессы изменяются во времени, зависит от того: обладают ли нелинейные элементы инерционностью или нет.

Нелинейные элементы называются инерционными, если их параметры не изменяются в течение периода изменения тока, поэтому их характеристики даются в виде зависимости между действующими значениями напряжения и тока (U=f(I)). Если параметры нелинейного элемента изменяются в течение периода изменения тока, то такие нелинейные элементы называются безынерционными. В рамках вопроса о том, является ли данный нелинейный элемент инерционным или безынерционным, имеется условность. Все зависит от величины частоты изменения тока. Один и тот же элемент, инерционный при больших частотах, может оказаться безынерционным при малых частотах.

П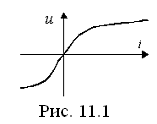 усть в цепи имеется безынерционный нелинейный элемент с характеристикой i=au³, показанной на рис. 11.1, а приложенное напряжение равно .

Тогда

.

Кривая тока приведена на рис. 11.2. Видно, что ток содержит третью гармонику.

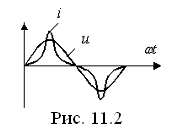
Из этого примера видно, что ток и напряжение на безынерционном элементе не могут быть одновременно синусоидальными. Главная особенность расчета в подобных случаях – это то, что расчет надо вести для мгновенных значений.

Теперь рассмотрим случай цепей, когда все нелинейные элементы являются инерционными. Параметры таких элементов не чувствуют изменений токов (напряжений) в течение периода, они реагируют лишь на изменение действующих значений токов (напряжений). Поэтому, если в цепи с инерционным нелинейным элементом действует синусоидальная ЭДС, то и ток также по форме будет синусоидальным. Следовательно, для расчета таких цепей можно использовать комплексный метод. Однако при изменении установившегося режима, например, вследствие изменения действующего значения приложенного напряжения, изменяются действующие значения токов и падений напряжения во всех ветвях, в том числе и в ветвях с нелинейными элементами. Так как у последних характеристики U=f(I) – нелинейные, то изменяются и параметры нелинейных элементов , , Поэтому исключается возможность использования метода наложения.

Остаются в силе законы Кирхгофа, но уравнения цепи, составленные на основе этих законов, являются нелинейными алгебраическими.

Для расчета этих уравнений можно использовать метод последовательных приближений. В этом методе задаются значения комплексных сопротивлений нелинейных элементов и, считая их постоянными, производится расчет цепей. Определив действующие значения токов и падений напряжения на нелинейных элементах, находят по характеристикам этих элементов их параметры, которые сопоставляют с первоначально заданными. При несовпадении вносят поправки в величины параметров и производят расчет заново до тех пор, пока принятые значения параметров не будут достаточно близки к их значениям, полученных из характеристик.