10.3. Характеристики намагничивания ферромагнетиков

Магнитная индукция в ферромагнитных веществах может иметь при одном и том же значении напряжённости тока различные значения, зависящие от предыдущих состояний материала.

Рассмотрим процесс намагничивания ферромагнитного вещества. Предположим, что вещество первоначально было полностью размагничено, т.е. результирующее поле элементарных токов было равно нулю.

При увеличении напряжённости внешнего поля индукция растёт сначала быстро вследствие того, что элементы тока ориентируются так, чтобы их магнитное поле совпало с внешним магнитным полем (рис. 10.10). При больших значениях индукции ( ) скорость её увеличения уменьшится. Магнитное состояние вещества приблизится к насыщению. При этом уже почти все элементарные токи ориентированы так, что их поля совпадают с внешним магнитным полем. Кривая OD₁, получающаяся при предварительно полном размагничивании вещества, называется начальной кривой намагничивания. Предположим, что H доведена до Н_m (точка D₁), а затем уменьшается. При этом кривая B=f(H) располагается выше начальной кривой намагничивания. При Н=0 наблюдается остаточная намагниченность и соответствующая ей остаточная индукция (элементарные токи в известной мере сохраняют упорядоченную ориентацию). Чтобы В=0, напряженность магнитного поля (Н) должна принять отрицательное значение, называемое коэрцитивной силой (в переводе с латинского языка – удерживающая сила). Если довести Н до отрицательного значения (-Н_m), то индукция примет отрицательное значение, соответствующее точке C₁. Вновь увеличивая Н до +Н_m, получим ветвь C₁D₂. Повторному уменьшению Н соответствует кривая D₂C₂ и т.д.

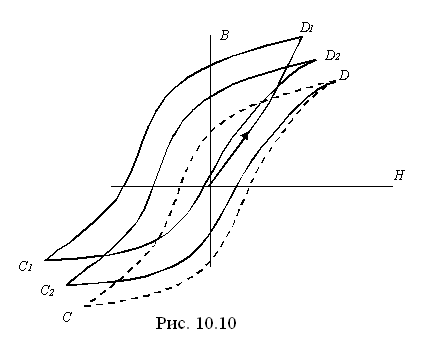
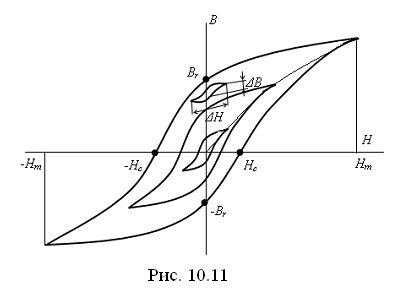
Таким образом, значение индукции при заданном значении H зависит от истории намагничивания. Это явление называется явлением магнитного гистерезиса. Только после достаточного числа (~10) перемагничиваний ферромагнитного материала получаем симметричную гистерезисную кривую CD (пунктирная линия). На рис. 10.11 показано семейство симметричных гистерезисных петель, полученных при различных значениях H_m. Кривая B=f(H), проходящая через вершины симметричных гистерезисных петель, называется основной кривой намагничивания и является вполне определённой для данного сорта материала. Поэтому магнитную проницаемость ферромагнитных материалов принято определять из основной кривой намагничивания. Точно так же остаточная индукция и коэрцитивная сила определяются из симметричной гистерезисной петли, причём H_m должно быть достаточно велика, чтобы магнитное состояние вещества было близко к состоянию магнитного насыщения. Часть петли, лежащей во втором квадрате и ограниченной изменением индукции от +B_r и Н=0 до В=0 и H=H_c, называют кривой размагничивания. Гистерезисная петля, одна из вершин которой лежит на кривой размагничивания, называется частным гистерезисным циклом или частной гистерезисной петлёй.

10. 4. Расчёт нелинейных магнитных цепей

М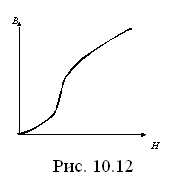 агнитные цепи в технических устройствах содержат участки из ферромагнитных материалов. Как показано на рис. 10.12 процесс намагничивания ферромагнитных материалов имеет специфический вид.

Т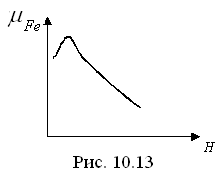 ак как (рис. 10.13), то нелинейное сопротивление не остаётся постоянным, заметно увеличиваясь в области насыщения. Поэтому магнитные цепи, содержащие ферромагнитные участки, при относительно сильных магнитных полях следует рассматривать как нелинейные. Методы расчёта таких цепей при пренебрежении потоками рассеяния аналогичны методам расчёта нелинейных электрических цепей.

А. Графический метод

1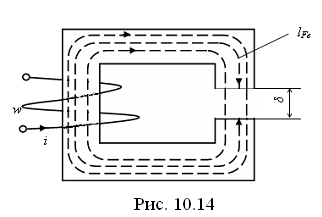 ) Рассмотрим магнитную цепь, показанную на рис. 10.14.

Электрический аналог приведен на рис. 10.15.

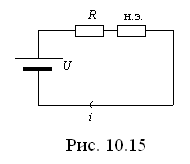
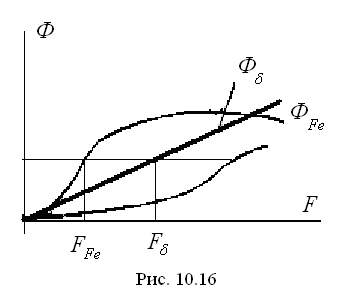
П ользуясь характеристикой намагничивания (рис. 10.12), строим кривую зависимости . Для этого ординаты кривой умножим на площадь поперечного сечения ферромагнитного сердечника и получим поток Ф_Fe,. Абсциссы умножим на l_Fe и получим МДС F. Используя полученные значения, строим зависимость (рис. 10.16). Зависимость для воздушного зазора представляется прямой, т.к. магнитная проницаемость воздуха величина постоянная, равная . Так как , то, складывая абсциссы построенных кривых, получаем , т.е. зависимость магнитного потока от полной МДС .

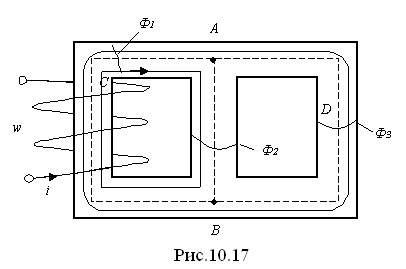
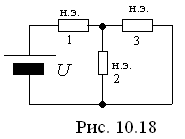
2). Необходимо рассчитать магнитную цепь, показанную на рис. 10.17. Кривая намагничивания ферромагнитного материала представлена на рис. 10.12. Электрический аналог показан на рис. 10.18.

Пользуясь характеристикой намагничивания по аналогии с предыдущим случаем, строим зависимости (рис. 10.19). Для этого для ряда точек зависимости умножаем ординату и абсциссу соответственно на S и на l и получаем соответствующие указанной точке значения магнитного потока Ф_i и МДС F_i, что даёт координаты точки i характеристики .

Так как и , то, складывая ординаты кривых 2 и 3, получим зависимость (кривая 4). Тем самым 2 и 3 ветви заменяем одной ветвью, включённой последовательно с участком 1. Теперь, складывая абсциссы кривых 4 и 5, получаем кривую 1 ( ), т.к.

.

Таким образом, получена зависимость магнитного потока в неразветвленной части цепи от полной МДС цепи.

Б. Численные методы

Для расчёта нелинейных магнитных цепей постоянного тока применимы все численные методы расчёта, описанные ранее при рассмотрении нелинейных электрических цепей постоянного тока.