
- •Часть 7 Учебное пособие
- •X. Линейные и нелинейные магнитные цепи постоянного тока
- •10.1. Связь между магнитным полем и электрическим током. Закон Био-Савара-Лапласа. Закон полного тока
- •10.2. Законы и параметры магнитных цепей
- •10.3. Характеристики намагничивания ферромагнетиков
- •10. 4. Расчёт нелинейных магнитных цепей
- •10.5. О расчёте постоянного магнита
- •XI. Нелинейные электрические и магнитные цепи при периодических процессах
- •11.1. Особенности периодических процессов в нелинейных цепях
- •11.2. Метод эквивалентных синусоид
- •11.3. Потери в ферромагнитном сердечнике при периодическом изменении магнитного потока
- •11.4. Уравнение и схема замещения катушки с ферромагнитным сердечником
- •11.5. Комплексное магнитное сопротивление
- •Комплексная проводимость равна
- •1I.6. Феррорезонанс при последовательном соединении катушки с ферромагнитным сердечником и конденсатора
- •11.7. Феррорезонанс при параллельном соединении катушки с ферромагнитным сердечником и конденсатора
- •11. 8. Управляемые индуктивные элементы. Ферромагнитный усилитель мощности
- •Расчет переходных процессов в нелинейных цепях
- •12.1. Графический метод расчета переходных процессов
- •12.2. Метод последовательных интервалов (метод Эйлера)
- •12.3. Метод расчета переходных процессов в нелинейной цепи, основанный на условной линеаризации уравнения цепи
- •12.4. Метод кусочно-линейной аппроксимации
- •Домашнее задание
- •Метод кусочно-линейной аппроксимации
- •Метод Эйлера
- •Приложение 6 Домашнее задание
- •Решение
- •Метод кусочно-линейной аппроксимации
- •Метод Эйлера
- •Приложение 7 Домашнее задание
- •Метод кусочно-линейной аппроксимации
- •Метод Эйлера
- •Дополнительная
Метод Эйлера
Находим
постоянную времени
,
аппроксимируя рабочий участок аб
одним отрезком
прямой. Находим соответствующую
индуктивность
![]() Гн.
Отсюда находим постоянную времени
Гн.
Отсюда находим постоянную времени
![]() .
.
Предполагаем, что переходный процесс длится .
Расчет выполняем с шагом , количество которых выбираем равным 16.
![]() .
.
Алгоритм расчета выглядит следующим образом (из уравнения (П.2.1))
![]() .
.
1).
Делаем нулевой шаг
![]()
2).
Делаем первый
шаг
,
![]() ,
,
![]() .
.
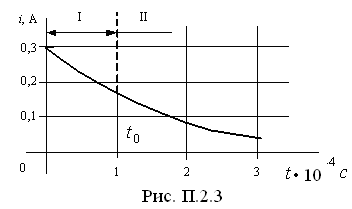
Аналогичным образом совершаем остальные 14 шагов.
По результатам расчетов строим зависимость (рис. П.2.3).
Приложение 7 Домашнее задание
«Расчет переходного процесса в цепи, содержащей нелинейный
конденсатор»

Дано:
,
,
![]() ,
,
![]() ,
схема цепи показана на рис. П.3.1.,
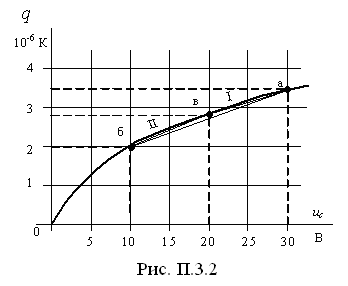
кулон-вольтная характеристика приведена
на рис. П.3.2.
,
схема цепи показана на рис. П.3.1.,
кулон-вольтная характеристика приведена
на рис. П.3.2.
Решение
1). - момент коммутации.
2). составим систему уравнений, используя законы Кирхгофа
 .
.
Преобразуем данную систему
![]() ,
,
![]() .
.
Подставим численные значения параметров и получим
![]() .
(П.3.1)
.
(П.3.1)
3). Определим рабочий участок на кулон-вольтной характеристике нелинейного сопротивления.
Находим
начальные условия:
![]() и по кулон-вольтной характеристике
находим
и по кулон-вольтной характеристике
находим
![]() .
Таким образом, мы нашли координаты
начала рабочего участка – точки а.
.
Таким образом, мы нашли координаты
начала рабочего участка – точки а.
Рассмотрим
установившийся режим. Из уравнения
(П.3.1) имеем
![]() .
Данное напряжение соответствует точке
б.
.
Данное напряжение соответствует точке
б.
Метод кусочно-линейной аппроксимации
Аппроксимируем
зависимость
![]() на участке aб
двумя
отрезками прямых aв
и вб.
на участке aб
двумя
отрезками прямых aв
и вб.
А).
Участок aв.
На этом
участке отрезок аппроксимирующей прямой
описывается следующим уравнением:
![]() .
Это уравнение вносим в уравнение (П.3.1)
и получаем
.
Это уравнение вносим в уравнение (П.3.1)
и получаем
![]()
![]()
![]() это уравнение решаем при начальном
значении напряжения на конденсаторе
это уравнение решаем при начальном
значении напряжения на конденсаторе
![]() .
.
Характеристическое
уравнение
![]() ,
отсюда
,
отсюда
![]() .
.
![]() .
.
Решение ищем в виде:
![]() ,
(П.3.2)
,
(П.3.2)
Для
получаем
![]() .
.
Запишем
формулу (П.3.2) для момента коммутации
![]() ,
,
![]() .
.
Формируем
решение
![]() .
.
Находим момент времени , соответствующий точке в:
![]() ,
,
![]() .
.
Таким образом, решение имеет вид с постоянной времени и действует в интервале .
Б). Участок вб.
На
участке вб
отрезок
прямой описывается уравнением
![]() .
Это выражение вносим в уравнение (П.3.1)
и получаем
.
Это выражение вносим в уравнение (П.3.1)
и получаем
![]() .
Характеристическое уравнение
.
Характеристическое уравнение
![]() ,
отсюда
,
отсюда
![]() ,
,
![]()
Решение ищем в виде:
. (П.3.3)
Для
получаем
![]() .
.
Запишем
формулу (П.3.3) для момента времени
![]() ,
,
![]() .
.
Формируем
решение
![]() .
.
Напряжение изменяется с постоянной времени на интервале времени .
Метод Эйлера
Находим
постоянную времени
,
аппроксимируя рабочий участок аб
одним
отрезком прямой, который описывается
следующим уравнением
![]() .
Данное выражение вносим в уравнение
(П.3.1) и получаем
.
Данное выражение вносим в уравнение
(П.3.1) и получаем
![]() .
Отсюда находим постоянную времени
.
Отсюда находим постоянную времени
![]() .
.
Предполагаем, что переходный процесс длится .
Расчет
выполняем с шагом
,
количество которых выбираем равным 16.
 .
.
Алгоритм расчета выглядит следующим образом (из уравнения (П.3.1))
![]() .
.
1).
Делаем нулевой шаг
![]()
2).
Делаем первый шаг
,
![]() ,
,
![]() .
.
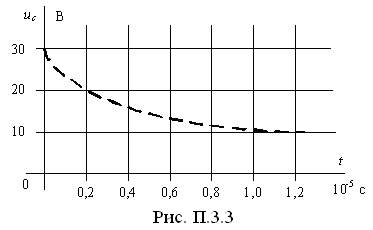
Аналогичным образом совершаем остальные 14 шагов.
По
результатам расчетов строим зависимость
![]() (рис.).
(рис.).
ЛИТЕРАТУРА
Основная
Нейман Л.Р., Демирчян К.С. ТОЭ. - Л.: Энергоиздат, 1981. - Т. 1,2.
Теоретические основы электротехники. Под ред. П.А. Ионкина. Т. 1,2. - М.: ВШ., 1976.
Теоретические основы электротехники. Под ред. Г.И. Атабекова. Т. 1,2 - М.: Энергия, 1979.
Сборник задач и упражнений по ТОЭ. Под ред. П.А. Ионкина. - М.: Энергоиздат, 1982. - 766с.
Пашенцев И.Д. Методические пособия по решению задач курса ТОЭ. - Л.: ЛИИЖТ, 1981. - Ч. I-VI.
Бессонов Л.А. Сборник задач по ТОЭ. - М.: ВШ, 1988.
Бессонов Л.А. Теоретические основы электротехники. - М.: ВШ, 1978. - Т.1,2.
Новгородцев А.Б. 30 лекций по теории электрических цепей. - СПб.: Политехника, 1995. - 519с.
Шимони К. Теоретическая электротехника. - М.: МИР, 1964. - .773с.
Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. - М.: Энергоиздат, 1989. - 333с.
Белецкий А.Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986. - 554с.
Поливанов К.М. Теоретические основы электротехники. - М.: Энергия, 1975. - Т.3. - 352с.
Ким К.К. Самоучитель по теории линейных электрических цепей- СПб.: ПГУПС, 2005. - Ч. 1, 2, 3, 4.
Литература информационно-методического обеспечения учебного процесса, разработанная кафедрой ТОЭ.
