Метод кусочно-линейной аппроксимации

Аппроксимируем зависимость на участке aв двумя отрезками прямых aб и бв.

А). Участок aб. На этом участке отрезок аппроксимирующей прямой описывается следующим уравнением . Это уравнение вносим в уравнение (П.1.1) и получаем , это уравнение решаем при начальном значении тока . , .

Характеристическое уравнение , отсюда .

Решение ищем в виде

. (П.1.3)

Для получаем .

Запишем уравнение (П.1.3) для момента коммутации , .

Формируем решение .

Находим момент времени , соответствующий точке б:

, .

Таким образом, решение имеет вид с постоянной времени , которое действует в интервале .

Б). Участок бв.

На участке бв отрезок прямой описывается уравнением . Это выражение вносим в уравнение (П.1.1) и получаем . Подставляем численные значения параметров и получаем . Данное уравнение решаем для , учитывая, что в установившемся режиме , и получаем

Характеристическое уравнение , отсюда .

Решение ищем в виде

, (П.1.4)

Для получаем .

Запишем уравнение (П.1.4) для момента времени , .

Формируем решение: .

Ток изменяется с постоянной времени на интервале времени .

Метод Эйлера

Находим постоянную времени , аппроксимируя рабочий участок ав одним отрезком прямой, который описывается следующим уравнением . Данное выражение вносим в уравнение (П.1.1) и получаем . Подставляем численные значения параметров цепи и получаем . Отсюда находим постоянную времени .

Предполагаем, что переходный процесс длится .

Расчет выполняем с шагом . Количество шагов выбираем равным 16.

.

Алгоритм расчета выглядит следующим образом:

.

Подставляем численные значения и получаем:

, .

1). Делаем нулевой шаг

2). Делаем первый шаг , , .

Аналогичным образом совершаем остальные 14 шагов.

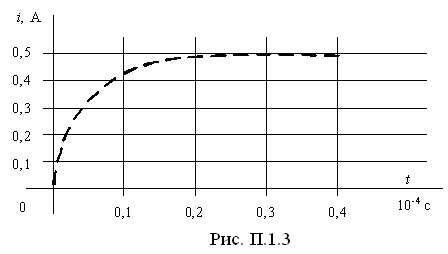
По результатам расчетов строим зависимость (рис. П.1.3).

Приложение 6 Домашнее задание

«Расчет переходного процесса в цепи, содержащей нелинейную

индуктивность»

Схема цепи показана на рис. П.2.1.

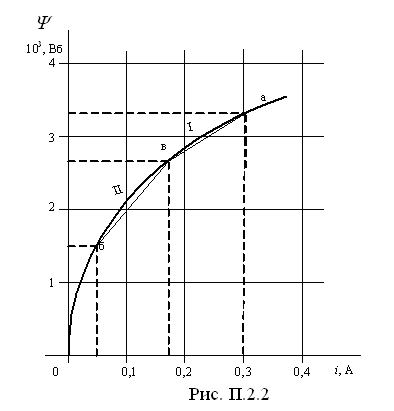
Дано: , , . Вебер-амперная характеристика представлена на рис.

Решение

1). - момент коммутации.

2). составим систему уравнений, используя законы Кирхгофа

.

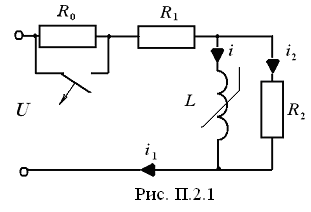
Преобразуем полученную систему уравнений следующим образом:

,

отсюда получим

.

Подставляем численные значения параметров и получим расчетное уравнение

. (П.2.1)

3). Определим рабочий участок на вебер-амперной характеристике нелинейной индуктивности (рис. П.2.2).

Находим начальные условия: , и далее по вебер-амперной характеристике находим

. (П.2.2).

- координаты начала рабочего участка – точки а.

Находим ток через нелинейную индуктивность в установившемся режиме, для . Из уравнения (П.2.1) имеем . Этот ток характеризует конец рабочего участка - точку в.

Метод кусочно-линейной аппроксимации

Аппроксимируем зависимость на участке aв двумя отрезками прямых бв и ва.

А). Участок вa. На этом участке отрезок аппроксимирующей прямой описывается следующим уравнением

. (П.2.3)

Это уравнение вносим в уравнение (П.2.1) и получаем , это уравнение решаем при начальном значении тока . Характеристическое уравнение , отсюда .

Решение ищем в виде:

, (П.2.4)

Для получаем .

Запишем уравнение (П.2.4) для момента коммутации , .

Формируем решение .

Это решение действует до и . Находим момент времени , соответствующий точке в:

, .

Таким образом, решение с постоянной времени действует в интервале .

Б). Участок вб.

На участке вб отрезок прямой описывается уравнением . Это выражение вносим в уравнение (П.2.1) и получаем . Данное уравнение решаем при .

Характеристическое уравнение , отсюда .

Решение ищем в виде:

, (П.2.5)

Для получаем .

Запишем формулу (П.2.5) для момента времени , .

Формируем решение .

Ток изменяется с постоянной времени на интервале времени .