8.2. Переходные процессы в неискажающей однородной линии (операторный метод расчета)
Т.к.
оригиналы
,
то операторные изображения равны
:
;
.
Производная
по времени имеет изображение:
,
- распределение
вдоль линии при
.
Производная по :
.
Для тока соответственно производные равны:
;
.
С учётом написанного уравнения однородной линии в операторном виде записываются следующим образом:
,
.
Полученные дифференциальные уравнения обыкновенные, т.к. содержат одну переменную .
Зададим
граничные условия:
и
,
примем нулевые начальные условия:
и
.
Уравнения принимают вид
;
.
Продифференцируем первое уравнение по и с учётом второго, получим
,
где
.
Решение для напряжения ищем в виде:
,
где
и
,
Операторный ток ищем в виде:
,
где
- операторное волновое (характеристическое)
сопротивление линии,
- операторный коэффициент распределения.
Для
неискажающей линии
данные выражения упрощаются:
,
.
Операторные напряжение и ток в этом
случае равны:
,
.
Перейдём к оригиналам, используя формулу Римана-Меллина
,
Здесь
член
представляет собой прямую волну
напряжения и тока, движущуюся со скоростью
от начала линии к её концу; член
- обратную волну, движущуюся со скоростью
от конца линии к её началу. В связи со
сказанным
напряжение
и ток в линии могут быть представлены
в виде суммы прямой и обратной волн. В
любой точке линии отношение напряжения
и тока для прямой волны равно
,
а для обратной волны -
.
Множитель
говорит о затухании волн по мере их
движения, причина которого – превращение
энергии электрического и магнитного
полей в теплоту.
8.3. Преломление и отражение волн в месте сопряжения двух однородных линий
Пусть
волна
доходит до места стыка двух однородных
линий, характеризующихся волновыми
сопротивлениями:
и
.
В дальнейшем все величины, относящиеся
к первой линии, будем снабжать индексом
1, ко второй – 2. Предположим, что до
подхода
,
во второй линии напряжения не было.
Волна
проходит стык, начинает распространяться
по второй линии, не меняя направление,
эта волна называется преломленной и
обозначается
.
Если
(линии не согласованы), часть волны
отразится от стыка и начинает
распространяться по первой линии в
обратную сторону, эта волна называется
отражённой и обозначается
.
Если
отражённой волны не возникает. Прямые,
преломлённые и отражённые волны связаны
друг с другом следующими соотношениями
в месте сопряжения линий:
,
.
Откуда получаем
;
;
;
.
Из
этих формул следует, что преломлённые
и отражённые волны имеют такую же форму,
что и падающие.
Величины
,
называются коэффициентами преломления,
величины
;
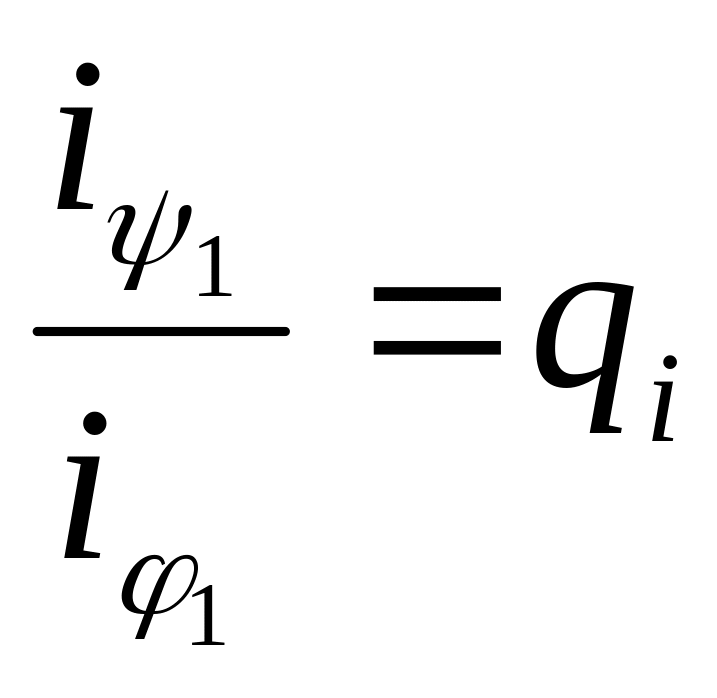- коэффициентами отражения.
И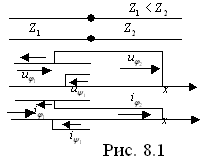
з
уравнений видно, что преломлённые и
падающие волны совпадают по знаку. Знак
отражённой волны зависит от соотношения
и
,
например, при
волна напряжения отражается без перемены
знака, а волна тока – с переменой.
Падающая волна тока в первой линии
уменьшается, а напряжения возрастает,
но не более чем в два раза (рис. 8.1).
Даже при очень больших значениях преломленная волна напряжения не может превышать падающую волну более чем в два раза.
П
ри
преломленная волна напряжения меньше
падающей, а преломленная волна тока
больше падающей. Волна напряжения меняет
знак, а волна тока нет (рис. 8.2). В результате
этого ток возрастает, но не более чем в
два раза.
Рассмотрим мгновенную мощность в месте стыка линий, имеем
,
и, следовательно,
или
.
Таким образом, если волна напряжения переходит из линии с малым волновым сопротивлением в линию с большим, напряжение увеличивается и в пределе может удвоиться.
Пример.
1) кабельная линия
воздушная линия;
2) линия передачи обмотка трансформатора.
Волны могут вызвать значительные перенапряжения между соседними точками цепи. Эти перенапряжения тем больше, чем круче фронт волны.