
- •Часть 6 Учебное пособие
- •VI. Синтез линейных электрических цепей с сосредоточенными параметрами
- •6.1. Свойства входных функций пассивных электрических цепей (двухполюсников)
- •6.2. Представление входных функций двухполюсников в виде простых дробей (метод Фостера)
- •6.3. Реализация входных функций двухполюсника, имеющих вещественные и мнимые корни знаменателя (метод Фостера)
- •VII. Электрические цепи с распределенными параметрами (установившиеся режимы)
- •7.1. Электрические цепи с распределенными параметрами
- •7.2. Уравнения линии с распределенными параметрами
- •7.3. Решение уравнений однородной линии
- •7.4. Бегущие волны
- •7.5. Характеристики однородной линии. Условия для неискажающей линии
- •7.6. Однородная линия при различных режимах работы
- •7.7. Режимы работы линии без потерь
- •8.2. Переходные процессы в неискажающей однородной линии (операторный метод расчета)
- •8.3. Преломление и отражение волн в месте сопряжения двух однородных линий
- •8.4. Отражение волн от конца линии
- •8.5. Включение однородной линии
- •8.7. Случай наличия активного сопротивления в месте стыка однородных линий
- •Для перехода волны через стык можно записать
- •IX. Нелинейные цепи при постоянном токе
- •9.1. Нелинейные элементы и их характеристики
- •9.4. Расчёт простых нелинейных цепей постоянного тока итерационным методом
- •В нулевом приближении каждый нелинейный элемент линеаризуется.
- •Другую схему вычислений можно представить уравнением
- •Рассмотрим ещё две схемы вычисления, вытекающие из уравнения
7.4. Бегущие волны
Рассмотрим уравнения (7.6) и введем обозначения
![]() ,
,
![]() .
.
При
![]() имеем
имеем
 .
.
Перейдем к оригиналам
![]() .
.
Видно,
что u
равно сумме двух составляющих
![]() и
и
![]() .
.
при x = const – синусоидальная функция времени.
Пусть
![]()
![]() ,
тогда, если t
= const,
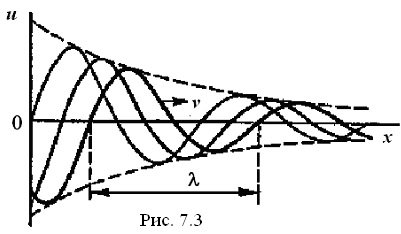
распределено вдоль линии по синусоидальному
закону с длиной волны
,
тогда, если t
= const,
распределено вдоль линии по синусоидальному
закону с длиной волны
![]() (рис.).
(рис.).
Говорят,
что волна напряжения движется вдоль
линии от начала к концу с постоянной
скоростью
![]() .
Т.к. при этом фаза колебания остается
неизменной,
.
Т.к. при этом фаза колебания остается
неизменной,
![]() называется фазовой
скоростью.
называется фазовой
скоростью.
Такого
рода волны называются бегущими
волнами. При
наличие множителя
![]() показывает, что амплитуда волны по мере
движения затухает по показательному
закону (
- коэффициент затухания). Т.к. фаза
напряжения изменяется с изменением x
, то коэффициент
,
характеризующий это изменение, называется
коэффициентом фазы.
показывает, что амплитуда волны по мере
движения затухает по показательному
закону (
- коэффициент затухания). Т.к. фаза
напряжения изменяется с изменением x
, то коэффициент
,
характеризующий это изменение, называется
коэффициентом фазы.
По
аналогии можно показать, что
![]() представляет собой волну длины
представляет собой волну длины
![]() ,
бегущую вдоль линии со скоростью
,
бегущую вдоль линии со скоростью
![]() ,
т.е. от конца к её началу. Амплитуда этой
волны затухает
,
т.е. от конца к её началу. Амплитуда этой
волны затухает
![]() по показательному закону по мере
продвижения от конца к началу.
по показательному закону по мере
продвижения от конца к началу.
Волна
![]() называется прямой
волной.
называется прямой
волной.
Волна
![]() называется обратной
волной.
называется обратной
волной.
Аналогично
можем записать для
![]()
![]() ,
где
,
где
![]()
![]()
или
для мгновенных значений
![]() ,
где
,
где
![]() - прямая волна,
- прямая волна,
![]() - обратная волна
- обратная волна
Найдём
![]() ;
;
![]() . (7.7)
. (7.7)
Физически объяснить появление обратных волн можно отражением прямых волн от конца линии. Поэтому прямые волны также называются падающими, а обратные – отражёнными. Их отношение называют коэффициентом отражения:
а) коэффициент отражения напряжения от конца линии:
 ,
,
б) коэффициент отражения тока от конца линии
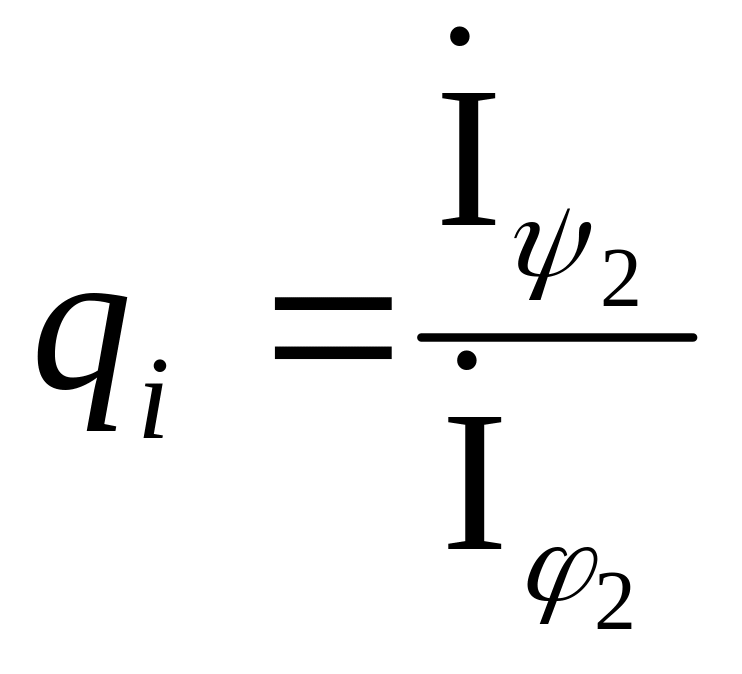 .
.
Предположим,
что линия с волновым сопротивлением
![]() замкнута на приёмник сопротивлением
замкнута на приёмник сопротивлением
![]() .
.
На конце линии имеем
![]() ;
;
![]() .
.
отсюда
![]() ;
;
![]() ;
;
где
 .
.
Разделив
первое равенство на второе (7.7), получим
![]() ,
т.е.
,
т.е.
![]() .
.
Рассмотрим частные случаи.
Если
 ;
;
 (отражённых волн нет), поэтому
(отражённых волн нет), поэтому
 .
.Если
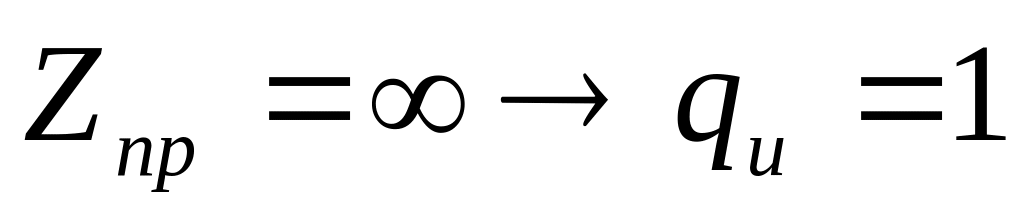 и
и
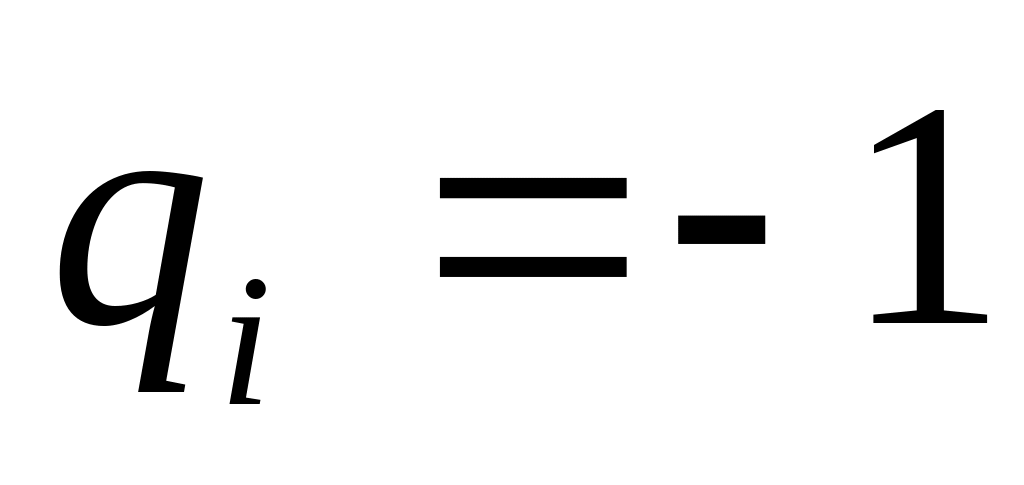 ,
следовательно:
,
следовательно:
а)
![]() ,
т.е. напряжение на конце линии
,
т.е. напряжение на конце линии
![]() удваивается по сравнению с падающей
волной,
удваивается по сравнению с падающей
волной,
б)
![]() ток в конце линии
ток в конце линии
![]() равен нулю.
равен нулю.
3)
![]() и
и
![]() .
.
![]() и
и
![]() ,
,
![]() и
и
![]() .
.
7.5. Характеристики однородной линии. Условия для неискажающей линии
Как
можно видеть, волновое сопротивление
линии
![]() и коэффициент распространения
и коэффициент распространения
![]() зависят от частоты. Поэтому условия
прохождения волн тока и напряжения
(различных гармоник) для разных частот
оказываются различными. Т.е. периодический
несинусоидальный
сигнал искажается при прохождении
линии. Чтобы сигнал не искажался,
необходимо, чтобы волновое сопротивление
,
коэффициент затухания
зависят от частоты. Поэтому условия
прохождения волн тока и напряжения
(различных гармоник) для разных частот
оказываются различными. Т.е. периодический
несинусоидальный
сигнал искажается при прохождении
линии. Чтобы сигнал не искажался,
необходимо, чтобы волновое сопротивление
,
коэффициент затухания
![]() и фазовая скорость
и фазовая скорость
![]() не зависели от частоты, а коэффициент
фазы
не зависели от частоты, а коэффициент
фазы
![]() был пропорционален частоте.
был пропорционален частоте.
Это выполняется, если соблюдено условие
![]() .
.
Действительно, при этом
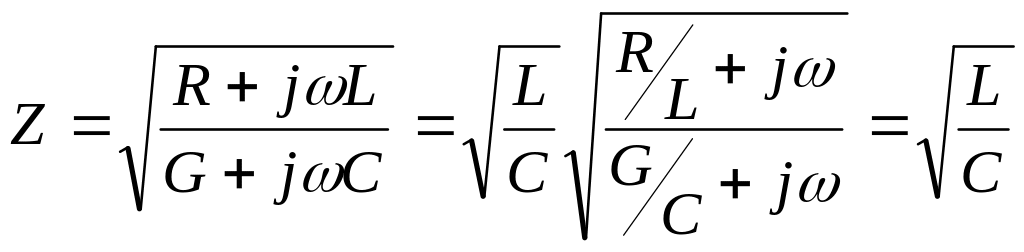 и
и
![]() .
.
При этих условиях коэффициент затухания и коэффициент фазы имеют минимальные значения.
![]() и
и
![]() ,
,
а
фазовая скорость – максимальна
![]() (равна скорости распространения волны
в диэлектрике, окружающем провода
линии).
(равна скорости распространения волны
в диэлектрике, окружающем провода
линии).
Для
воздушных линий
![]() Ом
и
Ом
и
![]() .
Для кабелей
.
Для кабелей
![]() Ом и
Ом и
![]() .
.
Длина
волны воздушной линии
![]() ;
при
;
при
![]()
![]() и на линии связи
можно укладывается несколько длин волн.
и на линии связи
можно укладывается несколько длин волн.
Обычно
в линиях
![]() (т.к.
(т.к.
![]() - мала), поэтому для достижения
искусственно увеличивают индуктивность,
включая в линию реактивные катушки или
применяя кабели, проводящие жилы которых
обмотаны тонкой лентой с большой
- мала), поэтому для достижения
искусственно увеличивают индуктивность,
включая в линию реактивные катушки или
применяя кабели, проводящие жилы которых
обмотаны тонкой лентой с большой
![]() .
Сигнал не искажается, если обеспечить
следующие условия:
.
Сигнал не искажается, если обеспечить
следующие условия:
![]() и
и
![]() ,
и к тому же не затухает.
,
и к тому же не затухает.
Чтобы сигналы передавались в приемник из линии без искажения нужно:
чтобы
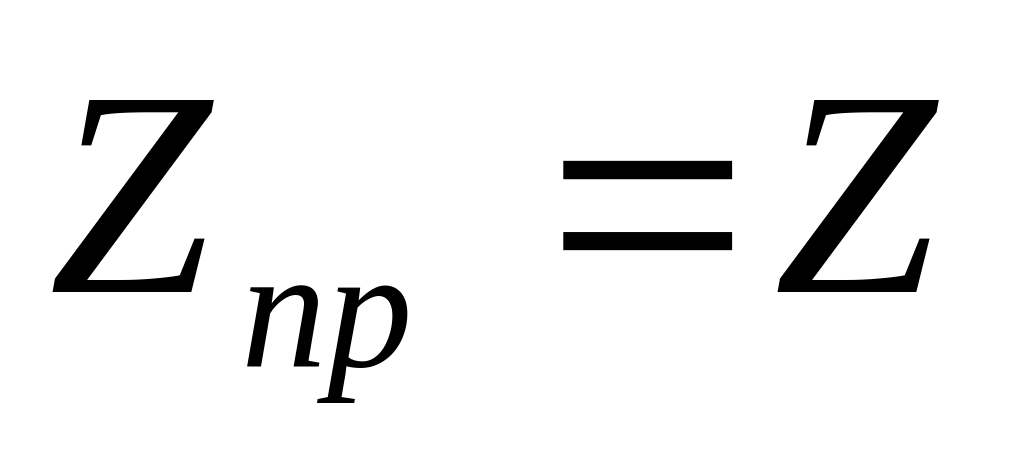 (приёмник и линия согласованы),
(приёмник и линия согласованы),если
 ,
нужно включать согласующее устройство,
например, трансформатор.
,
нужно включать согласующее устройство,
например, трансформатор.
