VII. Электрические цепи с распределенными параметрами (установившиеся режимы)
7.1. Электрические цепи с распределенными параметрами
В предыдущих семестрах рассматривались цепи с сосредоточенными параметрами, т.е. допускалось, что R, L и C сосредоточены на определенных участках цепи (резисторах, катушках и конденсаторах).
В случаях, когда время распространения электромагнитных волн вдоль цепи сравнимо со временем, в течение которого ток и напряжение изменяются на величину, составляющую заметную долю от их полного изменения в рассматриваемом процессе, упомянутого допущения делать нельзя. Т.е. цепь необходимо рассматривать как цепь с распределенными параметрами. В этом случае ток и напряжение являются функциями двух независимых переменных: t (времени) и x (координаты). Уравнения, описывающие процессы в этих цепях, – уравнения в частных производных.
Примеры цепей с распределенными параметрами:
ЛЭП,
Линии связи,
Высокочастотные коаксиальные линии связи,
Обмотки трансформаторов и электрических машин (при воздействии импульсного напряжения).
Е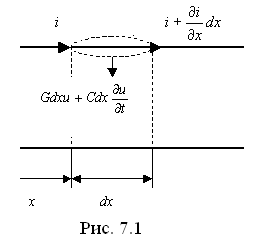
сли
параметры цепи распределены равномерно
по длине, то такие цепи (линии) называются
однородными.
Для однородных линий вводятся понятия
погонных параметров: L,
C,
R,
G
и M
на единицу длины линии.
В
инженерных расчетах зависимость
параметров от частоты не учитывается
.
7.2. Уравнения линии с распределенными параметрами
Рассмотрим двухпроводную однородную линию (рис. 7.1).
Здесь L, R – индуктивность и сопротивление пары проводов на единицу длины линии. C, G – емкость и проводимость утечки между проводами на единицу длины линии. Координата x отсчитывается от начала линии.
Согласно принципу непрерывности тока запишем уравнение для поверхности S:
,
здесь
- ток смещения,
- ток проводимости.
Данное уравнение преобразуется к виду
.
(7.1)
Н
апряжение
между проводами зависит не только от
t,
но и от x,
т.к. на каждом отрезке линии
имеет место падение напряжения в двух
проводах линии
(рис. 7.2). Это
падение напряжения складывается из
падения напряжения
на сопротивлении
пары проводов и падения напряжения
,
обусловленного индуктивностью
пары проводов, т.е.
.
Рассмотрим контур (рис.) и по II закону Кирхгофа запишем
или
.
(7.2)
В общем случае n–проводной линии, расположенной в воздухе над поверхностью земли, для каждого из проводов в этих уравнениях необходимо учитывать ЭДС взаимоиндукции и токи смещения между рассматриваемым проводом и соседними проводами. Тогда получаем 2n, так называемых телеграфных уравнений
,
,
здесь k – номер провода, все параметры определены с учетом земли.
7.3. Решение уравнений однородной линии
(установившийся синусоидальный режим)
Допустим, что ток и напряжение изменяются с частотой . Запишем уравнение линии, используя комплексный метод
,
(7.3)
,
(7.4)
т.к.
напряжение и ток зависят только от
координаты
,
=
f
(x),
вместо частных производных запишем
полные.
Дифференцируем (7.3) по x и используем (7.4)
,
где
.
Решение имеет вид
.
(7.5)
Из (7.3)
,
где
,
-
коэффициент распределения линии, Z
– волновое или характеристическое
сопротивление линии,
- коэффициент затухания (
),
- коэффициент фазы (
).
Будем
обозначать величины тока и напряжения
в начале линии (x
= 0) с индексом «1» , а в конце линии (x
=
)
– c
индексом «2».
Найдем
и
в уравнении (7.5), для этого рассмотрим
начало линии.
При
x
= 0
и
,
отсюда получим
и
.
Следовательно
,
.
(7.6)
или (с учетом тригонометрических функций)
,
.
Значение
и
(конец
линии) получается, если положить x
=
.
,
.
Из
этих уравнений выразим
и
через
и
,
.
Последние два уравнения - уравнения четырехполюсника в А – параметрах.
Постоянные этого четырехполюсника равны
;
;
,
причем
.
Как и любой четырехполюсник, линия может быть представлена Т или П-образной эквивалентной схемой.
Представлять линию Т или П-образной эквивалентной схемой целесообразно, если нас интересуют только ток и напряжение на входе и выходе линии. Если необходимо знать распределение тока и напряжения вдоль линии, то ее эквивалентируют цепной схемой. Чем больше звеньев, тем точнее решение (обычно берут 10 – 20 звеньев).