6.2. Представление входных функций двухполюсников в виде простых дробей (метод Фостера)

Входную функцию , являющуюся рациональной дробью, можно представить в виде суммы члена и простых дробей:

,

где - корни . При этом ,если n = m + 1. и при n = m. Когда n = m - 1, коэффициенты . При n = m + 1 , коэффициенты определяется после выделения по известному способу.

Рассмотрим случай, когда корни мнимые и вещественные.

Мнимые корни должны быть попарно сопряжены. Пусть и . При этом должно быть и . Поэтому

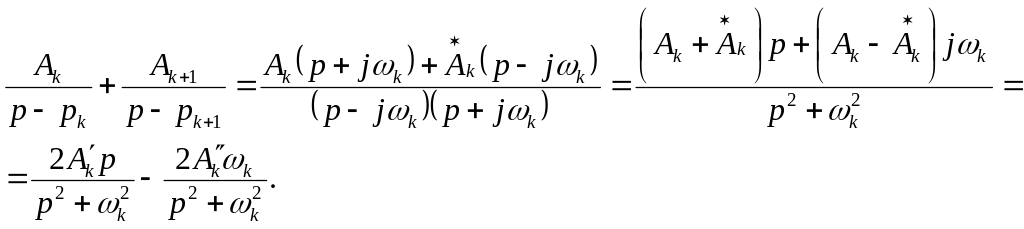
Если при , то . В самом деле, пусть , тогда из условия следует, что и, следовательно, . Пусть теперь и , т.е. . Тогда из следует, что , т.е. . Оба неравенства для удовлетворяются только при . Поэтому

,

где - вещественное число. Если корень вещественный, то соответствующая ему дробь имеет вид: т.е. при наличии только вещественных и мнимых корнях имеем

. (6.2)

6.3. Реализация входных функций двухполюсника, имеющих вещественные и мнимые корни знаменателя (метод Фостера)

Пусть в уравнении (6.2) F(p) представляет входное операторное сопротивление двухполюсника, . Далее предположим, что все коэффициенты в (6.2) вещественны и положительны. Рассмотрим, как могут быть реализованы отдельные члены (6.2).

Слагаемое реализуется с помощью катушки с индуктивностью , т.к. операторное сопротивление для нее равно .

С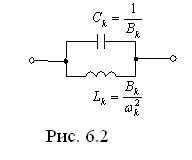 лагаемое реализуется резистором с активным сопротивлением . Слагаемое реализуется с помощью участка цепи, показанного на рис. 6.2.

Слагаемое 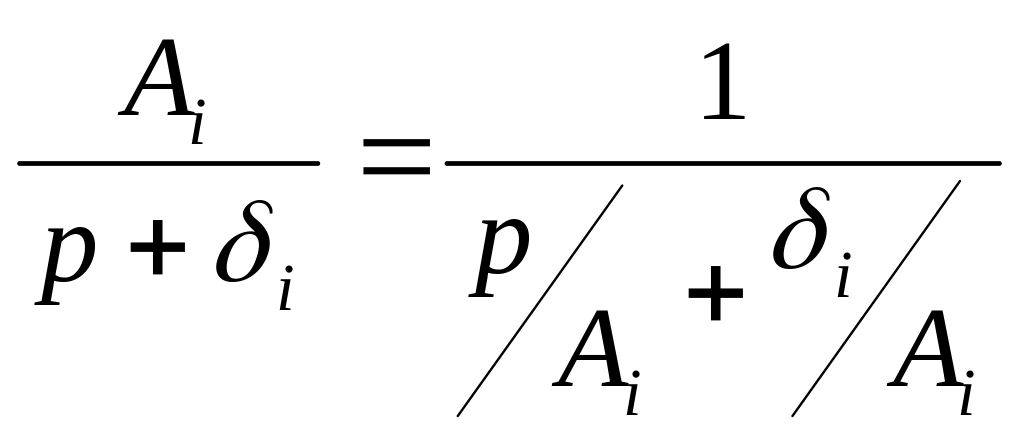реализуется участком цепи, приведенном на рис. 6.3.

Т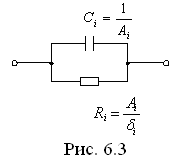 аким образом, для конкретного случая можно записать . Данное выражение соответствует цепи, показанной на рис. 6.4.

Пусть в соотношении (6.2) F(p) выражает входную операторную проводимость, . Тогда слагаемое реализуется с помощью конденсатора , т.к. операторная проводимость для него .

Слагаемое реализуется участком цепи с активной проводимостью .

С лагаемое реализуется участком цепи, который показан на рис. 6.5,

т .к. операторная проводимость для него равна

.

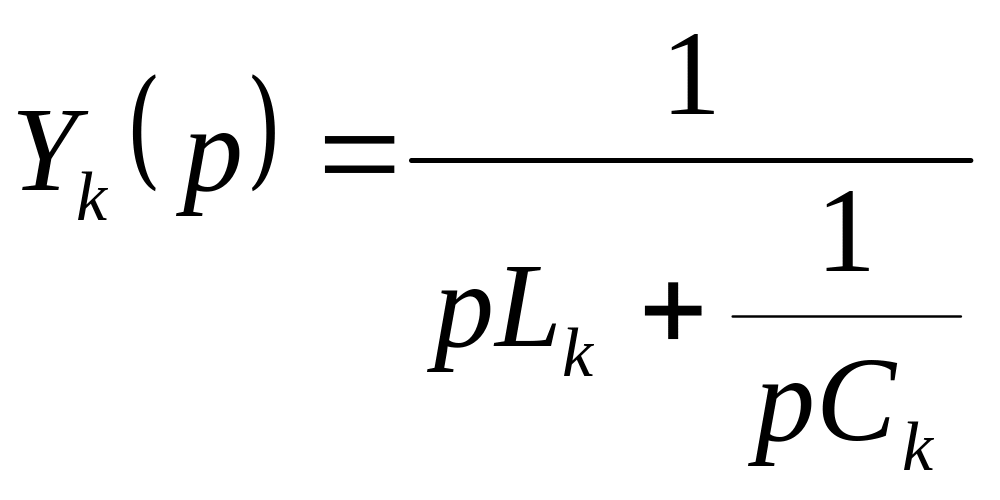Слагаемое реализуется участком цепи (рис. 6.6),

т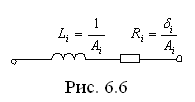 .к. его операторная проводимость определяется следующим выражением .

Т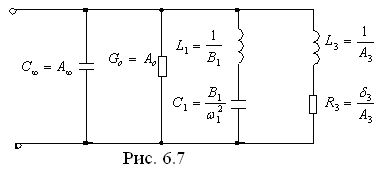 аким образом, для конкретного случая можно записать

и в соответствии с этим выражением имеем следующую цепь (рис. 6.7).

В некоторых частных случаях при отрицательном значении возможна реализация с помощью выражения (6.2), если - достаточно большая величина

.

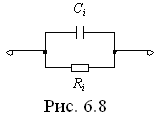
Если , то слагаемое реализуется в виде схемы (рис. 6.8)

либо в виде схемы, показанной на рис. 6.9.

Д робь 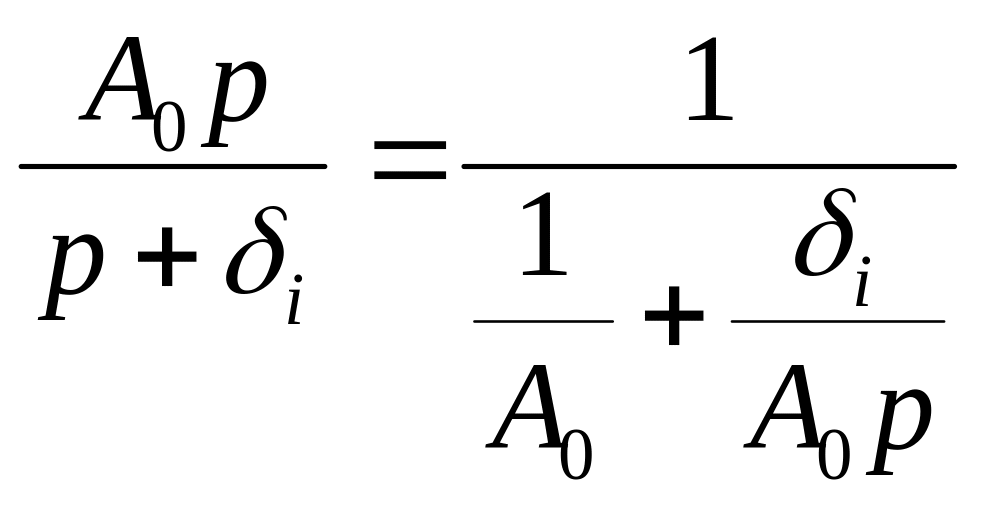в случае реализуется участком цепи (рис. 6.10), т.к. для него

.

В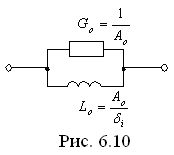 случае эта дробь реализуется следующей цепью (рис. 6.11).

Рассмотрим пример реализации . Принято сопротивление R, , , и частоту выражать в относительных единицах, для того чтобы коэффициенты полиномов были небольшими.

Пусть .

Знаменатель имеет только мнимые корни , .

Поэтому , ; .

Кроме того, (в этом убеждаемся, положив p = 0 в выражении для ).

; .

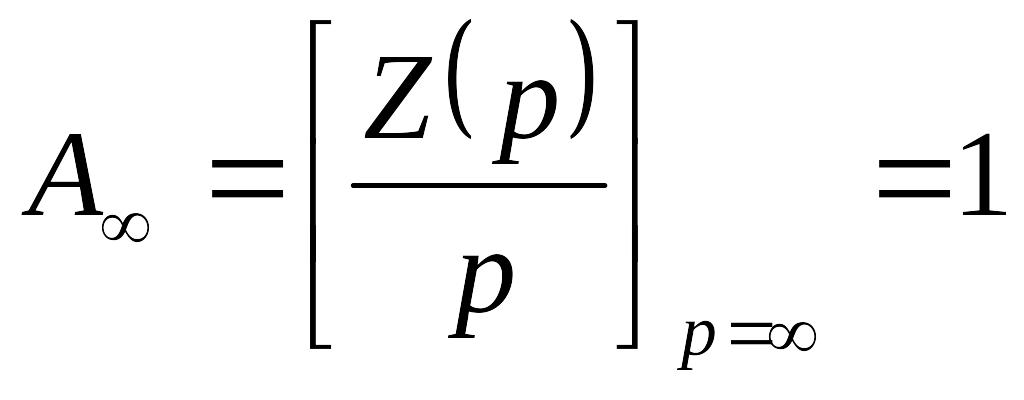Аналогично получаем

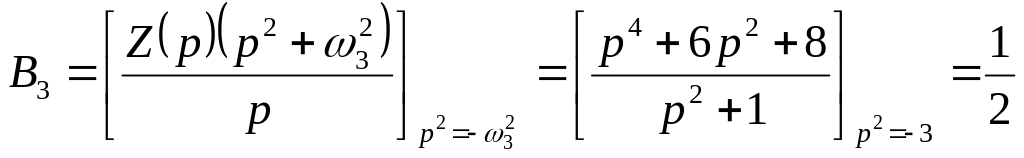
Таким образом, параметры схемы (рис. 6.12), реализуют заданную функцию .

_{Г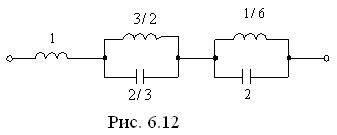 де} ; ; ; ; .

Рассмотрим теперь операторную проводимость

.

В данном случае , т.к. - правильная дробь.

; ;

имеем схему, показанную на рис. 6.13,

г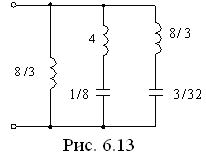 де ; ; ; ; .

6.4. Реализация входных функций двухполюсника, имеющих только мнимые корни знаменателя

Если знаменатель входных функций и имеет только мнимые корни, то соответствующая цепь состоит только из реактивных элементов. Поэтому в выражении (6.2) должны отсутствовать члены и , т.к. при их реализации должны быть использованы активные сопротивления. В соответствии со сказанным должна иметь вид:

.

Отсюда видно, что если все , то будет полным полиномом от четных степеней , т.е. полиномом, содержащим все, без пропуска, четные показатели от 0 до “m”. При этом будет полным полиномом нечетных степеней. Учитывая это, запишем

,

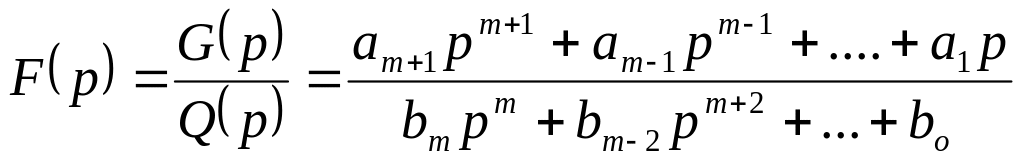где m – четное число.

Значение p = 0 является нулем . Если один из корней равен нулю, то . При этом, сокращая числитель и знаменатель на , получим - полином четных степеней, - полином нечетных степеней.

Для возможности реализации в виде электрической цепи, состоящей из реактивных элементов, необходимо, чтобы она удовлетворяла указанным выше требованиям, а именно: степени полиномов и должны отличаться друг от друга на единицу; нули и полюсы должны чередоваться, т.е.

, .

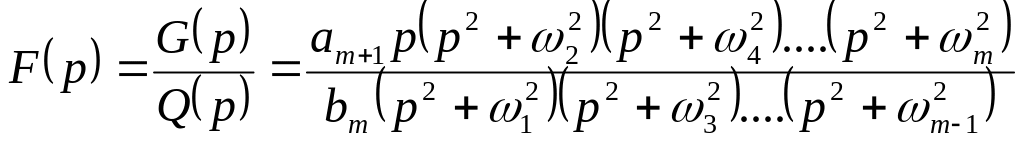Если эти условия выполнены, то возможна реализация . Существуют различные методы реализации.

Метод Фостера заключается в представлении в виде выражения (6.2). Цепи, реализующие каждое слагаемое в (6.2), были рассмотрены выше.

Неудобство метода – необходимость определения корней знаменателя.

В методе Кауэра необходимость в определении корней знаменателя отпадает. Суть этого метода состоит в постепенном выделении частей вида или сначала из , а затем из остатков после выделения предыдущей части, с последующей реализацией выделяемых частей в виде индуктивной катушки или конденсатора.

Пусть имеет полюс . Это означает, что степень полинома числителя на единицу больше степени полинома знаменателя. Предположим . Разделив числитель и знаменатель, выделяем целую часть . Получаем

.

В степень полинома в знаменателе на единицу больше. Следовательно, обратная функция имеет степень числителя на единицу больше степени знаменателя. Следовательно

.

По аналогии далее получаем .

Эту процедуру продолжаем до тех пор, пока остаток не будет равен нулю. В соответствии с такой операции можно представить в виде цепной дроби

.

Отсюда видно, что можно реализовать с помощью схемы (рис. 6.14).

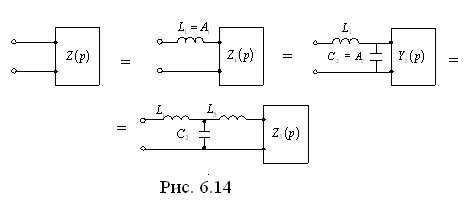
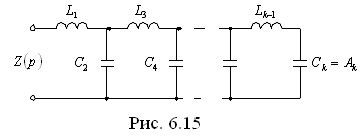
Если k – четное (k – показатель числителя), то цепь будет выглядеть, как показана на рис. 6.15, если k – нечетное, то – как на рис. 6.16.

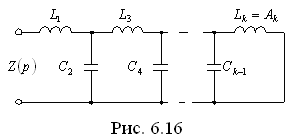
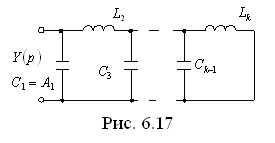
Если и степень полинома на единицу больше степени полинома , то, поступая аналогично, получили бы для случая k – четное цепь, показанную на рис. 6.17, или для k – нечетное – цепь, представленную на рис. 6.18.

Если степень числителя «n» меньше степени знаменателя на единицу, то, добавив в числителе член с , можно формально пользоваться тем же методом. Однако в данном случае будет , т.е. в схемах рис. 6.15-6.16 будем иметь , а в схемах рис. 6.17-6.18 .

Рассмотрим теперь случай, когда имеет полюс . Это означает, что полином знаменателя нечетной степени, а полином числителя четной степени, при этом степень полинома знаменателя на единицу меньше степени полинома числителя. В этом случае постепенно выделяется , и получаемая при этом цепная дробь имеет вид:

.

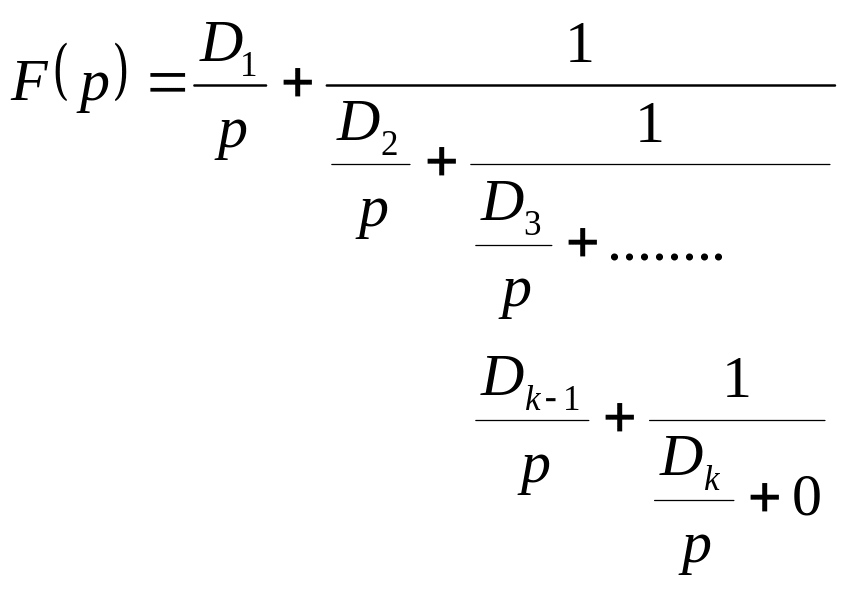Пример.

Имеется входная функция цепи .. Необходимо построить схему цепи.

Представим функцию цепи в виде ,

где ; .

Найдем проводимость ; ,

где .

; ,

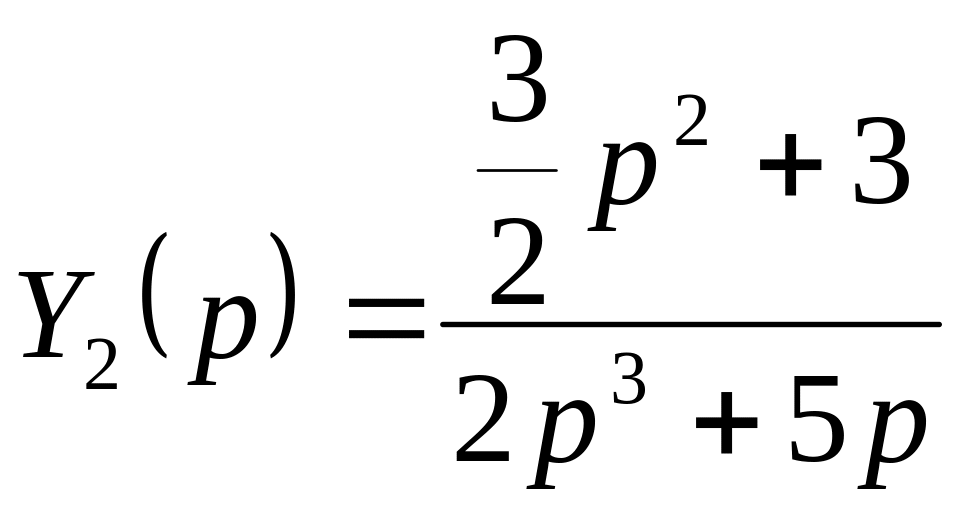где ; .

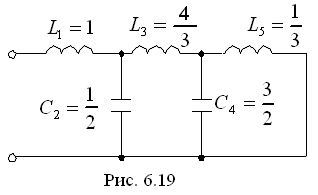
Таким образом, имеем следующие параметры цепи: ; ; ; ; и схему (рис. 6.19)

6.5. Реализация входной функции, имеющей комплексные

корни

Пусть числитель и знаменатель имеют комплексные корни. Для реализации используем метод Бруне. Согласно этому методу приведем к виду минимального активного сопротивления, т.е. к виду ,где

Для определения частоты , при которой , найдем вещественную часть .

Вещественная часть при , т.е. определяется следующим образом. Эта часть, как рациональная дробь, должна иметь члены с четными показателями относительно , т.к. только в этом случае при функция будет вещественной. Поэтому представим в виде суммы рациональных дробей, состоящих из членов с четными и нечетными показателями.

. Так как , то, умножив числитель и знаменатель на , получим

,

где .

Согласно этой формуле для рассматриваемого случая имеем

.

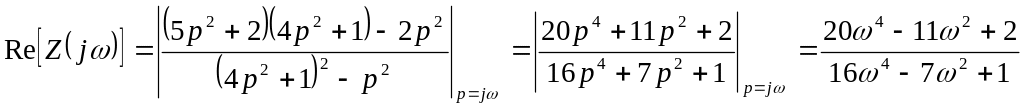Возьмем производную и определим экстремумы функции

.

Отсюда находим . Этой частоте соответствует .

Таким образом, имеем .

При имеем , где . Тогда можно представить в виде (соответствующая схема цепи показана на рис. 6.20), где .

П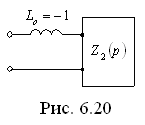 ри имеем , ,

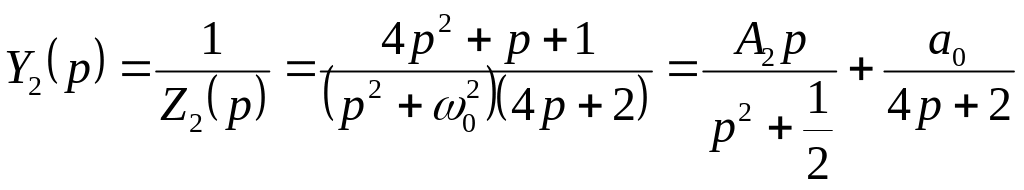где ; .

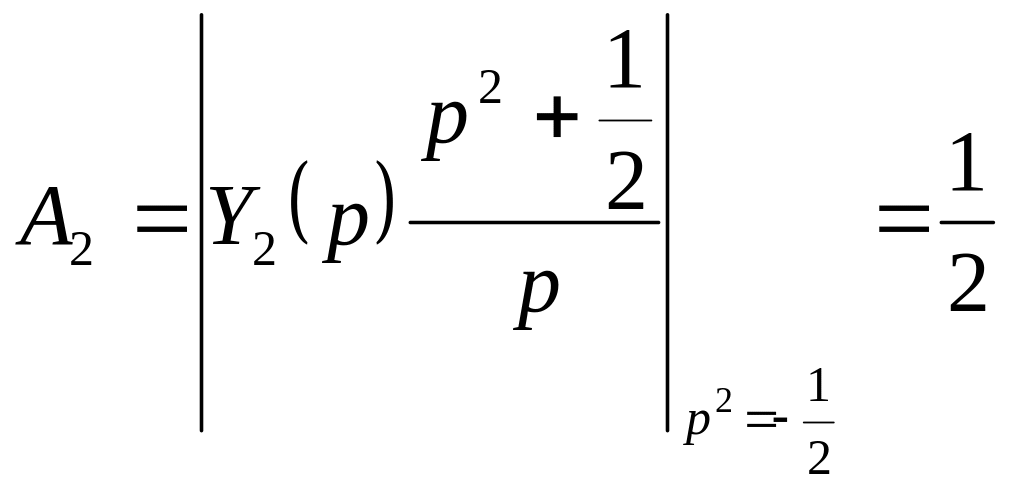Поэтому .

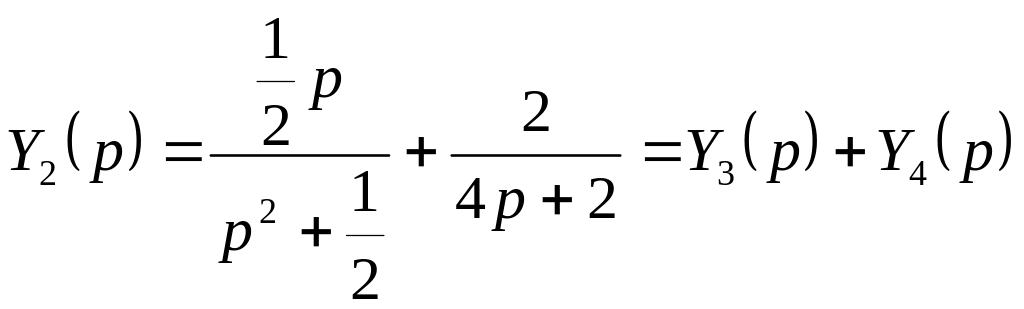Реализация выполняется ранее изложенным методом в виде последовательной цепи из и , а реализация - в виде последовательной цепи из и , т.к. .

Результирующая цепь, соответствующая входной функции , приведена на рис. 6.21.

Отрицательную индуктивность можно реализовать введением в цепь трансформатора с коэффициентом связи .