VI. Синтез линейных электрических цепей с сосредоточенными параметрами

Задача анализа – расчет токов, напряжений в заданной цепи. В предыдущих семестрах мы рассматривали только эту задачу.

Задача синтеза – построить электрическую цепь, процессы в которой будут протекать по наперед заданному закону.

Ставится задача, построить цепь (двухполюсник) с требуемыми характеристиками из линейных элементов. Известны входная величина и ее операторное изображение ( - ток или напряжение). Задан требуемый закон изменения входной величины , операторное изображение которой т.е. имеет выражение для передаточной функции , которой должна обладать создаваемая цепь. Задача, следовательно, заключается в построении электрической цепи по заданной передаточной функции или по заданной частотной характеристике . Входные сопротивления и проводимость двухполюсника можно рассматривать как частные случаи передаточной функции. Для этого одну из двух входных величин (ток или напряжение) нужно принять за входную, а другую – за выходную. Входные и передаточные функции цепи называют просто функциями цепи и обозначают .

для линейных цепей с сосредоточенными параметрами являются рациональными дробями комплексной частоты . Свойства и свойства описываемых ими электрических цепей однозначно определяются расположением нулей и полюсов . могут быть заданы в виде частотных характеристик.

При анализе электрических цепей мы видели, что различные электрические цепи могут иметь одинаковую по виду функцию цепи (например, дифференцирующие цепи, состоящие из R, L и R, C; интегрирующие цепи из тех же элементов). Отсюда видно, что одна и та же задача синтеза может иметь различные решения. Возможны также случаи, когда решение конкретной задачи синтеза с помощью линейных пассивных элементов (R, L, C) может отсутствовать.

В связи с этим возникают следующие основные вопросы синтеза цепи по заданной функции цепи :

1. Выявление возможностей реализации цепи по заданной с помощью обычных элементов – R, L, C.

2. Разработка метода конкретной реализации заданной в виде физической цепи.

6.1. Свойства входных функций пассивных электрических цепей (двухполюсников)

Основные свойства входных операторных сопротивлений и проводимостей пассивных электрических цепей (т.е. цепей из R, L, C):

1. и - вещественны при вещественных значениях . Полиномы в числителе и знаменателе функций и - вещественны, т.к. они образуются суммами, разностями, произведениями и частными от деления вещественных параметров R, L, C участков цепи.

2. Полюсы и нули функций и располагаются только в левой полуплоскости или на оси мнимых, т.е. , причем, в случае полюсы и нули простые. При этом все коэффициенты полиномов от , стоящих в числителе и знаменателе, положительны.

Действительно:

.

Для каждой пары комплексных корней и имеются множители

и для вещественных корней множители вида . Отсюда видно, что если все и , то множители, на которые разлагается полином, не содержат отрицательных чисел, следовательно, коэффициенты , , ... , - положительные числа.

3. Вещественная часть функций и не отритцательна (т.е. положительна или равна нулю): и , если .

Пусть ,т.е. . В этом случае и являются обычными комплексными сопротивлением и проводимостью. При наличии активного сопротивления, хотя бы в одной ветви двухполюсника, активная мощность на входе двухполюсника положительна и, следовательно, активное сопротивление и активная проводимость всего двухполюсника также положительны, т.е. и .

К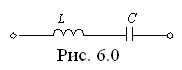 огда в цепи имеются только реактивные элементы, то . Покажем, что даже для чисто реактивной цепи, если . Для цепи, показанной на рис. 6.0.

. (6.1)

Это выражение по форме совпадает с выражением для комплексного сопротивления цепи

.

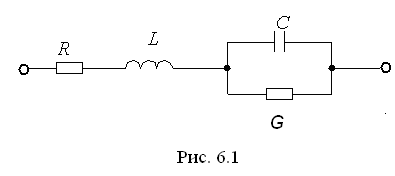
Эта цепь приведена на рис. 6.1.

Комплексное сопротивление при и имеет вещественную часть больше нуля, точно так же и вещественная часть операторного сопротивления (6.1) при больше нуля. Для любой сложной цепи, состоящей только из реактивных элементов, по аналогии, может быть построена цепь, содержащая активные элементы, причем, последовательно с катушкой добавляется активное сопротивление и параллельно каждому конденсатору добавляется проводимость . При этом операторное входное сопротивление реактивной цепи при и будет по форме аналогично комплексному сопротивлению всей цепи с добавленными активными элементами.

Функции, обладающие указанными выше свойствами, называются положительными вещественными функциями.

Из изложенного следует, что для того чтобы рациональная дробь

представляла операторное выражение входной функции и могла быть реализована в виде конкретной электрической цепи, она должна удовлетворять выше перечисленным требованиям, т.е. и должны иметь нули в левой полуплоскости или на оси мнимых чисел, все коэффициенты и должны быть вещественны и положительны и, наконец, должно выполняться неравенство при .

Кроме того, степени полиномов «n» и «m» не должны отличаться друг от друга более чем на единицу.