9.4. Расчёт простых нелинейных цепей постоянного тока итерационным методом

Термин «итерация» происходит от латинского слова и означает «повторение».

Для расчёта цепей с нелинейными элементами очень часто применяют итерационный метод решения нелинейных алгебраических уравнений.

Для уяснения сущности метода рассмотрим эквивалентную схему, на которой источник ЭДС Е и сопротивление r_в (рис. 9.22) представляют произвольную линейную часть первоначальной схемы, т.е. представляют некоторый эквивалентный источник.

Пусть внешняя характеристика эквивалентного источника совпадает с прямой 1 (рис. 9.23), а характеристика нелинейного элемента даётся кривой 2.

Если решение производить геометрическим путем, то точка “а” пересечения характеристик определяет режим цепи, т.е. напряжение и ток в этом режиме.

Е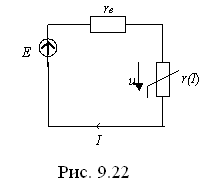 сли данную задачу решать численным способом, например итерационным методом, необходимо поступить следующим образом:

1. Совершаем, так называемое, нулевое приближение. Для этого задаём напряжение U₀ равное, например, Е и по кривой 2 находим ток I₀.

В нулевом приближении каждый нелинейный элемент линеаризуется.

2. По уравнению

(9.1)

н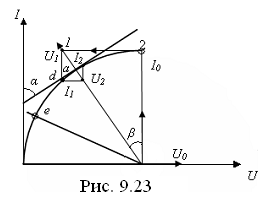 аходим уточнённое значение напряжения U₁ (т.е. делаем первое приближение).

3. Находим по характеристике 2 новое значение I₁ и т.д.

Из рис. следует, что итерационный процесс сходится к искомым значениям тока и напряжения в точке «а». В курсе математики доказывается, что условие сходимости состоит в выполнении неравенства

в окрестности искомого режима (точка «а») и что, чем меньше значение , тем быстрее сходится процесс.

Так как , то имеем следующее условие сходимости

. (9.2)

Т.к. r_д в некотором масштабе определяется tg, а r_в в том же масштабе - tgβ, то в окрестности точки «а» условие (9.2) выполняется.

Другую схему вычислений можно представить уравнением

. (9.3)

В этом случае задаются током I и по кривой 2 находят значение напряжения U, а по формуле (9.3) – уточнение значения тока. Затем по характеристике 2 находят новое значение напряжения и т.д. Применив эту схему выражения для определения тока и напряжения, соответствующих режиму в точке «а», можно показать, что итерационный процесс расходится. Дело в том, что для схемы вычисления по уравнению (9.3) условия сходимости другие, а именно

Так как , то имеем следующее условие сходимости

. (9.4)

Условие (9.4) является условием сходимости второй схемы вычисления. Решение для этой схемы вычисления сходится при определении тока и напряжения, соответствующих режиму в точке «е».

Рассмотрим ещё две схемы вычисления, вытекающие из уравнения

, (9.5)

где r(I) - статическое сопротивление нелинейного элемента. Для применения уравнения (5) целесообразно предварительно построить характеристику в зависимости от I. Тогда следует такая схема расчёта: зададимся r(I) и находим из уравнения (9.5) ток, затем по характеристике r(I) – уточнённое значение r(I) и соответствующий ему ток по уравнению (9.5) и так далее. Найдём условия сходимости при указанной схеме вычисления.

. (9.6)

Так как ,

то

. (9.7)

Подставим (9.7) в (9.6) и учтём уравнение (9.5), получим

. (9.8)

Из рис. 9.24 следует, что для вольт-амперной характеристики с положительным r_д(I) и убывающим r(I) (кривая 1) имеет место r_д(I) < r(I), поэтому условие (9.8) сходимости выполняется при любом значении r_в.

Для ВАХ с возрастающим статическим сопротивлением (кривая 2) расчётное уравнение должно быть составлено относительно напряжения на нелинейном элементе

. (9.9)

Условие сходимости

. (9.10)

Так как ,

отсюда

. (9.11)

Подставляем (9.11) в (9.10) и учтём уравнение (9.9), в результате получим

. (9.12)

Для ВАХ с положительным r_д(U) и возрастающим r(U) имеет место r(U) < r_д(U), и условие (9.12) выполняется при любом r_в. Быстрота сходимости итерационного процесса зависит от вида ВАХ, выбора начальных приближений и r_в. Однако основным фактором, определяющим решение нелинейных уравнений итерационным методом, является составление расчётных уравнений – схем вычисления. Поскольку в схемах вычисления по уравнениям (9.5) и (9.9) итерационный процесс сходится при любом r_в, это дает основание применить данный метод для расчёта разветвленной цепи с любым числом пассивно нелинейных элементов.

В заключении отметим, что существуют ещё численные методы - методы Зейделя и Ньютона.

ЛИТЕРАТУРА

Основная

1. Нейман Л.Р., Демирчян К.С. ТОЭ. - Л.: Энергоиздат, 1981. - Т. 1,2.

2. Теоретические основы электротехники. Под ред. П.А. Ионкина. Т. 1,2. - М.: ВШ., 1976.

3. Теоретические основы электротехники. Под ред. Г.И. Атабекова. Т. 1,2 - М.: Энергия, 1979.

4. Сборник задач и упражнений по ТОЭ. Под ред. П.А. Ионкина. - М.: Энергоиздат, 1982. - 766с.

5. Пашенцев И.Д. Методические пособия по решению задач курса ТОЭ. - Л.: ЛИИЖТ, 1981. - Ч. I-VI.

6. Бессонов Л.А. Сборник задач по ТОЭ. - М.: ВШ, 1988.

7. Бессонов Л.А. Теоретические основы электротехники. - М.: ВШ, 1978. - Т.1,2.

8. Новгородцев А.Б. 30 лекций по теории электрических цепей. - СПб.: Политехника, 1995. - 519с.

9. Шимони К. Теоретическая электротехника. - М.: МИР, 1964. - .773с.

10. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. - М.: Энергоиздат, 1989. - 333с.

11. Белецкий А.Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986. - 554с.

12. Поливанов К.М. Теоретические основы электротехники. - М.: Энергия, 1975. - Т.3. - 352с.

13. Ким К.К. Самоучитель по теории линейных электрических цепей- СПб.: ПГУПС, 2005. - Ч. 1, 2, 3, 4.

14. Литература информационно-методического обеспечения учебного процесса, разработанная кафедрой ТОЭ.

Дополнительная

1. Матханов П.Н. Основы анализа электрических цепей. - М.: ВШ, 1990

2. Практикум по ТОЭ. Под ред. Шакирова М.А. - СПб.: СПбГТУ, 1995. - Ч. 1, 2, 3.

3. Шебес М.Р. Задачник про теории линейных электрических цепей. - М.:ВШ, 1973. - 655с.

4. Демирчян К.С., Бутырин П.Л. Моделирование и машинный расчет электрических цепей. - М.: ВШ, 1988.

5. Кухаркин Е.С. Основы технической электродинамики. - М.: ВШ, 1969 - Ч. 1, 2.

Рекомендуется использование пакетов программ Pspice, Workbench, Matlab, Mathcad, Elcat.

60