Nieobciążoność

Estymator jest nieobciążony jeżeli:

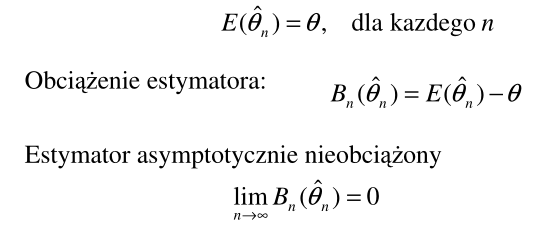
Interpretacja

Własność nieobciążoności oznacza, że przy wielokrotnym losowaniu próby średnia z wartości przyjmowanych przez estymator nieobciążony równa się wartości szacowanego parametru. Własność ta gwarantuje otrzymanie za jego pomocą ocen wolnych od błędu systematycznego.

Zgodność i nieobciążoność

Współzależności pomiędzy własnościami zgodności i nieobciążoności:

• jeżeli estymator θn parametru jest zgodny, to równocześnie jest asymtotycznie nieobciążony; twierdzenie odwrotne nie jest prawdziwe

• jżeli estymator θn parametru θ jest nieobciążony (lub asymptotycznie nieobciążony) oraz jeżeli jego wariancja w miarę wzrostu liczebno?ci próby zmierza do zera, to θn jest estymatorem zgodnym

9. Jak bada się efektywnośćestymatora określonego parametru populacji generalnej. Jak interprytuje się twz. Błąd estymatora

Aby ułatwić opis populacji wyróżnia się jej cechy (np. wzrost osobników, ich masę). Cechę można traktować jako zmienną losową, a wartości cechy poszczególnych elementów populacji – jako realizacje zmiennej losowej. Stąd też do charakterystyki populacji używamy wszystkich tych pojęć, które charakteryzują zmienną losową; możemy w szczególności określić rozkład populacji i parametry tego rozkładu.

Wartości parametrów charakteryzujących populację na ogół nie są znane, można je jednak w przybliżeniu oszacować na podstawie próby. Tak otrzymaną wartość nazywamy estymatorem danego parametru. Jeżeli x₁, x₂, ..., x_n oznaczają wartości poszczególnych elementów próby, to estymatorem wartości średniej (oczekiwanej) cechy X w populacji jestśrednia arytmetyczna elementów próby:   

[1]

natomiast estymatorem wariancji jest wariancja z próby:   

[2]

W konkretnej próbie otrzymamy konkretną wartość estymatora (ocenę parametru). Jednak dla różnych prób pobranych z tej samej populacji uzyska się na ogół inne oceny, ponieważ próby są kompletowane losowo i jest rzeczą przypadku, które elementy populacji zostaną pobrane. Estymator danego parametru można zatem traktować jako zmienną losową, a ta ma swoją wartość oczekiwaną i wariancję. Standardowe odchylenie estymatora nazywa się jego błędem standardowym.

Wielkość będącą funkcją elementów próby (tzn. określoną na podstawie elementów próby), nazywamy statystyką, a więc każdy estymator jest statystyką.

Jeden parametr może mieć wiele estymatorów. Estymatorem wartości oczekiwanej, na przykład, jest nie tylko średnia arytmetyczna, ale również modalna (wartość najczęstsza w próbie) czy też mediana.   

Medianą nazywa się wartość środkowego elementu próby uporządkowanej według wartości rozpatrywanej cechy; gdy liczba elementów próby jest parzysta, za medianę się przyjmuje średnią arytmetyczną wartości elementów środkowych; np. w 6-elementowej próbie o wartościach: 3, 5, 5, 8, 9, 9 mediana jest równa: (5+8)/2 = 6,5.

Nie ma jednego kryterium, które pozwoliłoby określić, który estymator danego parametru jest najlepszy.; Wyróżnia się kilka kryteriów porównawczych, spośród których omówimy tutaj 3 najważniejsze.

Nieobciążoność. Estymator t danego parametru  jest nieobciążony, jeżeli jego wartość oczekiwana jest równa wartości parametru w populacji:   

E(t) =  .

Gdy estymator jest nieobciążony, to po wyborze bardzo (nieskończenie) wielu prób losowych z populacji i ocenie parametru w każdej z nich okaże się, że średnia tych ocen jest równa wartości parametru w populacji. Średnia arytmetyczna (wzór [1]) jest estymatorem nieobciążonym wartości średniej populacji,  , natomiast wariancja dana wzorem [2] własności takiej nie ma; estymatorem nieobciążonym wariancji  ² jest:   

[3]

Zgodność. Estymator nazywamy zgodnym, jeżeli wraz ze wzrostem liczebności próby wartość estymatora zbliża się dowolnie blisko do wartości parametru w populacji. Estymatorami zgodnymi są zarówno średnia arytmetyczna, jak i wariancje dane wzorami [2] i [3].

Efektywność. Miarą efektywności estymatora jest jego błąd standardowy. Mały błąd standardowy oznacza, że oceny parametru uzyskane z różnych prób (tej samej wielkości) będą bardzo skupione wokół wartości parametru w populacji. Estymator o najmniejszym błędzie standardowym nazywa się estymatorem najefektywniejszym. Najefektywniejszym estymatorem wartości średniej w populacji jest średnia arytmetyczna.