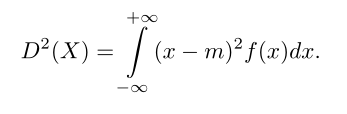4.Na czym polega standartyzacja zmiennej w rozkładzie normalnym.Podaj funkcję gęstości zmiennej standartyzowanej

Aby mówić o rozkładzie normalnym standaryzowanym, należy w pierwszym rzędzie zająć się zagadnieniem standaryzacji zmiennej losowej. Proces ten jest nieskomplikowany, polega on bowiem na odnalezieniu standaryzowanej zmiennej U, co jest niczym innym, jak obliczeniem jej odchylenia standardowego i kolejnym ilorazom, różnicy każdej z osobna realizacji zmiennej X i jej średniej arytmetycznej, co zapisać można w postaci:U = (X - m)/Odchylenie standardowe_X. Standaryzowany rozkład normalny SN jest określany w całości przez dwa parametry, a mianowicie; wartość oczekiwaną E(U) = 0 oraz przez wariancję i odchylenie standardowe równe:D²(U) = D(U) = 1. W rezultacie procesu standaryzacji zmiennej losowej ,b>X_C otrzymujemy transformację rozkładu normalnego z danymi parametrami na standaryzowany rozkład normalny z parametrami określonymi liczbowo, czyli N(0,1), dla którego funkcja gęstości F(u)u przybiera następującą postać:   dla wszystkich możliwych realizacji zmiennej standaryzowanej U.

Szczególnie ważne znaczenie ma w praktyce dystrybuanta zmiennej standaryzowanej U, definiowana podobnie, jak dystrybuanta rozkładu normalnego, czyli:   z tym, jednak iż:     Poziomy dystrybuant można odczytywać z tablic statystycznych posługując się zależnością następującą; dla u większego od 0  

 

5.Jak oblicza się wartość średnia (nadzieję matematyczną) w przypadku zmiennej Losowej skokowej i ciąglej

Wartość oczekiwaną często - potocznie - nazywa się wartością średnią.

Wartość oczekiwana

— Wartością oczekiwaną (wartością przeciętną, wartością średnią, nadzieją matematyczną) zmiennej losowej Xtypu skokowego o rozkładzie pi= P(X = xi), gdzie i ∈ {1,2,...}, nazywamy liczbę

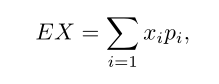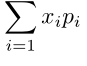przy założeniu, że suma jest skończona albo szereg nieskończony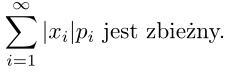

Wartość oczekiwana

— Wartością oczekiwaną zmiennej losowej X typu ciągłego o funkcji gęstości prawdopodobieństwa f nazywamy liczbę

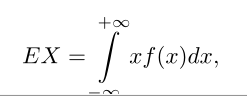
przy założeniu, że całka

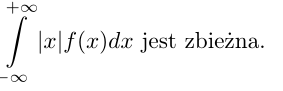
Podstawowe własności wartości oczekiwanej

— E(aX + b) = aEX + b, gdzie a,b ∈ R

— jeżeli X i Y są dowolnymi zmiennymi losowymi, dla których istnieją wartości oczekiwane EX oraz EY , to E(X +Y ) = EX + EY

— jeżeli istnieje E|X|, to prawdziwa jest nierówność |EX| ? E|X|

— wartość oczekiwana jest miarą położenia, parametrem pozycyjnym: wskazuje punkt środkowy rozkładu, tzn. punkt,wokół którego grupują się wartości zmiennej losowej

— interpretacja fizyczna: wartość oczekiwaną można utożsamiać z pojęciem środka ciężkości, jeśli prawdopodobieństwa zinterpretujemy jako masy

Uwaga. Jak wynika z definicji, wartość oczekiwana dla niektórych zmiennych losowych nie istnieje (odpowiedni szereglub odpowiednia całka nie są zbieżne)

6. Jak oblicza się wariację zmiennej Losowej skokowej I ciąglej

Wariancja

— Wariancją zmiennej losowej X nazywamy liczbę

— Jeżeli X jest zmienną losową typu skokowego o rozkładzie pi= P(X = xi), i ∈ {1,2,...}, i wartości oczekiwanej EX = m, to

— Jeżeli X jest zmienną losową typu ciągłego o funkcji gęstości prawdopodobieństwa f i wartości oczekiwanej EX =m, to