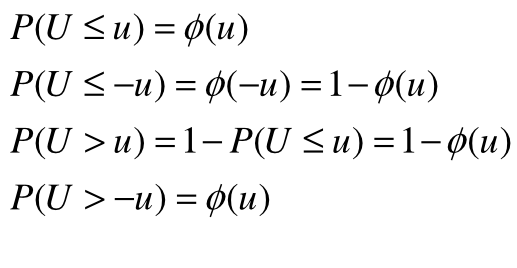1.Przedstaw rozkład dwuminowy (Bernoulliego). Podaj zawożenia tego rozkładu I wyjaśnij wszystkie symbole.

Jeżeli chcemy określić prawdopodobieństwo wystąpienia k razy określonego zdarzenia w n niezależnych doświadczeniach, przy danym prawdopodobieństwie p wystąpienia tegoż zdarzenia w pojedynczym doświadczeniu korzystamy z rozkładu dwumianowego:

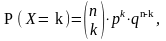
gdzie: n - ilość niezależnych doświadczeń ogółem,

p - prawdopodobieństwo wystąpienia zdarzenia w pojedynczym doświadczeniu,

q - prawdopodobieństwo niewystąpienia zdarzenia w pojedynczym doświadczeniu,

k - ilość doświadczeń w których ma wystąpić dane zdarzenie.

Jeżeli: p = q to rozkład jest symetryczny

p < q to rozkład jest prawostronnie asymetryczny

p > q to rozkład jest lewostronnie asymetryczny

Dla rozkładu dwumianowego zachodzi:

E(X) =

Wartość przeciętna zmiennej losowej.

Zdefiniujmy zmienną losową Y równą liczbie sukcesów k w N doświadczeniach. Każdy z wyników otrzymanych w pojedynczym doświadczeniu zależy od innej zmiennej losowej Z, mającej dwie realizacje Z: Z={0, 1}.

Y	Z	realizacje zmiennej losowej Z
y0=0,	z1, z2, z3, ..., zN	0, 0, 0, ..., 0
y1=1,	z1, z2, z3, ..., zN	0, 0, 1, ..., 0
y2=2,	z1, z2, z3, ..., zN	1, 0, 1, ..., 0
...,	...,	...,
yn=N,	z1, z2, z3,...zN	1, 1, 1, ..., 1

Wariancja zmiennej losowej.

2. Przedstaw rozkład Poissona. Podaj zawożenia tego rozkładu I wyjaśnij wszystkie symbole.

Rozkład Poissona stanowi szczególny przypadek rozkładu dwumianowego (Bernoulliego), w którym prawdopodobieństwo sukcesu (p) jest bardzo małe, a liczba niezależnych doświadczeń (N) na tyle duża, że iloczyn:

jest wielkością stałą, dodatnią i niezbyt dużą.

gdzie e = 2,718 (podstawa logarytmu naturalnego)

k – liczba realizacji elementów wyróżnionych w doświadczeniu

Wartość przeciętna zmiennej losowej.

Wariancja zmiennej losowej.

Rozkład Poissona stosujemy wszędzie tam, gdzie liczba obserwowanych doświadczeń niezależnych N w przestrzeni lub czasie jest bardzo duża, a prawdopodobieństwo sukcesu w pojedyńczym doświadczeniu p bardzo małe. Przykłady: - rozpad promieniotwórczy: liczba jąder n duża, prawdopodobieństwo rozpadu konkretnego jądra bardzo małe; - zderzenia cząstek elementarnych, duża ilość cząstek, mała szansa na zderzenie;

3. Przedstaw rozkład normalny (Caussa Larlace’a).Podaj ego własności I wyjaśnij wszystkie symbole we wzorze na funkcję gęstości prawdopodobięstwa.

Rozkład zwany rozkładem Gaussa-Laplace'a jest najczęściej spotykanym rozkładem zmiennej losowej ciągłej.Mówimy, że zmienna losowa ciągła X ma rozkład

normalny o wartości oczekiwanej µ i odchyleniu standardowym σ

X ~ N (µ σ)

Rozkład prawdopodobieństwa w przypadku zmiennej losowej ciągłej nosi nazwę rozkładu (funkcji) gęstości. Funkcja gęstości w rozkładzie normalnym o postaci:

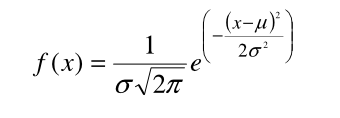określona została dla wszystkich rzeczywistych wartości

zmiennej X.

Funkcja gęstości w rozkładzie normalnym:

- jest symetryczna względem prostej x = µ

- w punkcie x = µ osiąga wartość maksymalną

- ramiona funkcji mają punkty przegięcia dla x = µ - σ

oraz x = µ + σ

- kształt funkcji gęstości zależy od wartości parametrów:

µ i σ. Parametr µ decyduje o przesunięciu krzywej,

natomiast parametr σ decyduje o „smukłości” krzywej.

Funkcja gęstości rozkładu normalnego ma zastosowanie do reguły „trzech sigma”, którą następnie rozwinięto na regułę „sześć sigma” – stosowaną w kontroli jakości, przede wszystkim w USA (np. General Electric, General Motors Company) Reguła „trzech sigma” - jeżeli zmienna losowa ma rozkład normalny to:

- 68,3 % populacji mieści się w przedziale (µ - σ; µ + σ)

- 95,5 % populacji mieści się w przedziale (µ - 2σ; µ + 2σ)

- 99,7 % populacji mieści się w przedziale (µ - 3σ; µ + 3σ)

Prawdopodobieństwo w rozkładzie normalnym wyznacza się dla wartości zmiennej losowej z określonego przedziału

Natomiast:

W celu obliczenia prawdopodobieństwa zmiennej X w

rozkładzie normalnym o dowolnej wartości oczekiwanej µ i odchyleniu standardowym σ dokonuje się standaryzacji. Standaryzacja polega na sprowadzeniu dowolnego rozkładu

normalnego o danych parametrach µ i σ do rozkładu standaryzowanego (modelowego) o wartości oczekiwanej µ = 0 i odchyleniu standardowym σ = 1. Zmienną losową X zastępujemy zmienną standaryzowaną U, która ma rozkład N(0,1)

Zatem :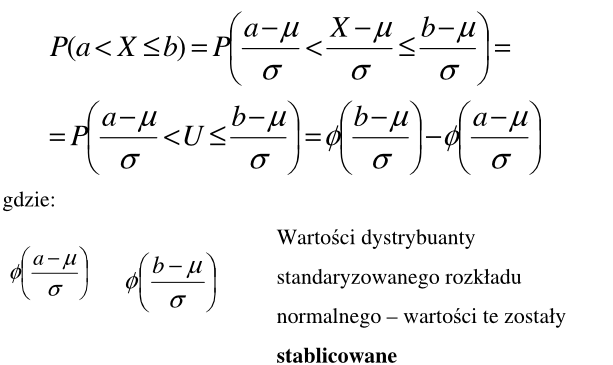

Własności dystrybuanty standaryzowanego rozkładu normalnego: