Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное

учреждение высшего профессионального образования

«Уральский Федеральный университет имени первого

Президента России Б.Н.Ельцина»

Факультет заочного обучения

Кафедра «Электроэнергетика и электротехника»

Контрольная работа

по дисциплине «Физика»

Вариант №2

Преподаватель С. И. Путков

Студент:

гр. ЭНЗ – 130301с – НЕ д Д. А. Баглай

Невьянск 2014

Задача №102

l = t + 3t²

R = 2м

t = 1cτ

Найти: 1) a - ? 2) d - ?

Решение:

Полное ускорение материальной точки, движущейся по окружности радиуса R равно: или , где нормальное ускорение, характеризующая изменение скорости материальной точки по направлению и равное по величине - тангенциальное ускорение, характеризующее изменение скорости по величине и равное по модулю, где E – угловое ускорение – первая производная от угловой скорости по времени t т.к.

- связь между угловой и линейной скоростью, где линейная скорость – первая производная от пути по времени t.

Так как – зависимость пути пройденного точкой по окружности от времени, то – зависимость скорости от времени t и тогда – зависимость угловой скорости от времени. (2)

Сделав подстановку (2) в уравнении (1) получим: - угловое ускорение.

Зная Е – угловое, найдем : тангенциальное ускорение. В момент времени t = 1c начала движения , тогда – нормальное ускорение.

Определим полное ускорение:

2) Найдем угол между нормальным и полным ускорением по формуле: , откуда

Ответ: 1) – полное ускорение материальной точки. 2) – угол между нормальным и полным ускорением.

Задача №112

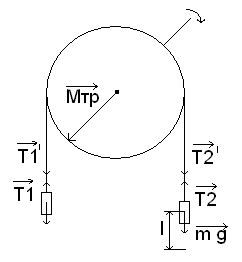
R = 0,2 м

У = 50 кг.м²

Мтр = 98,1 Н м

Е = 2, 36 1/c²

t = 1с

Найти: 1) T1 – T2 - ? 2) l - ?

Блок с двумя подвешенными грузами одной массы совершает вращательное движение. Запишем для него основное уравнение динамики вращательное движения: (1) , У где – момент инерции блока; - угловое ускорение;

- момент сил, действующих на него, равный (2) где и – моменты сил натяжения со стороны гирь; - момент силы трения.

Подставим (2) в уравнения (1):

В скалярном виде откуда – разность сил натяжения нити по обе стороны блока.

т.к а то

2) Определим расстояние l, на которое переместится гиря за время t по формуле равноускоренного движения из состояния покоя ( ): , где а – ускорение грузов.

Силы натяжения и приложены в точках, где шнур отходит от тела. Эти точки шнура участвуют в двух движениях: вращательном и поступательном, поэтому для тех можно записать:

Линейное ускорение тела а совпадает с тангенциальным линейным ускорением , поэтому

- расстояние, на которое переместится каждая гиря за время t

Ответ: 1) – разности сил натяжения по обе стороны блока;

2) l = 0,0236м – перемещение грузов за t = 1c.

Задача №122

М = 0,5т = 500 кг

m = 120 кг

h1 = 5м

h2 = 4см = 0,04 м

Найти: 1) - ? 2) <F>c - ?

1) при неупругом ударе выполняется закон сохранения импульса: где – импульс бойка перед ударом; - импульс бойка и свои после неупругого удара.

Спроецируем вектора на ось ох: , откуда (1) скорости бойка и свал после удара, где – скорость бойка перед ударом, которую найдем по формуле: т.к. боёк движется под действием силы тяжести, участвуя в свободном падении. Сделав подстановку в формуле (1), получим:

- кинетическая энергия бойка и свал после удара.

Определим – к.п.д. неупругого удара, считая полезной энергию, затраченную на вбивания свал: , где Wкол – полезная энергия, которая определяется кинетической энергией свала и бойка:

Wзатр - энергия затраченная, определяется потенциальной энергией бойка:

Сделаем подстановку:

- к.п.д. неупругого удара

2) Определяем среднюю силу сопротивления грунта с помощью закона сохранения энергии: где А – работа неконсервативных сил – силы трения, равная

- полная механическая энергия бойка и свал в ( )1 после удара, равная – полная механическая энергия бойка и свал в ( )2, равная 0.

Тогда откуда

– средняя сила сопротивления грунта

Ответ: 1) – к.п.д. удара; 2) - средняя сила сопротивления грунта при вбивании сваи.

Задача №142

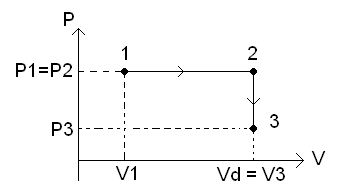
p = const

∆T1 = 100K

Q12 = 4,2 кДж

V = const

Q23 = -5,04 кДж

P3 =

T2 = 400К

Найти: 1) 2) 3)

1) Переходя из состояния 1 в состояние 3, газ участвует в двух процессах: 1 – 2 – изобарное расширение; 2 – 3 – изохорное охлаждение.

Запишем первое начало термодинамики для изобарного процесса:

(1) - изменение внутренней энергии, где i – число силе печей свободы данного газа; V – количество вещества – работа при изобарном процессе.

Сделаем подстановку в уравнение (1):

(2) – количество теплоты полученное газом при p = const.

Для изохорного процесса первое начало термодинамики имеет вид: , где – изменение внутренней энергии. Так при этом процессе давление уменьшается в 2 раза, а по закону Шарля

Таким образом , откуда – количества вещества

Подставим V в уравнение (2):

Так как – коэффициент Пуассона для газа, то , откуда – коэффициент Пуассона

- коэффициент Пуассона

Так как , то , откуда

i = 3 число степеней свободы данного газа

Определим V – количества вещества:

2) Найдем изменение энергии ∆S газа для каждого из изопроцессов и всего процесса в целом

Запишем второе начало термодинамики: где ∆S – изменение энтропии; приведенное количество теплоты

т.к. для изобарного процесса , то , где

– молярная теплоемкость при постоянном давлении.

Для изохорного процесса , поэтому , где – молярная теплоемкость при постоянном объеме – изменение энергии при изохорном охлаждении.

Определим изменение энтропии на всем процесс:

Ответ: 1) – коэффициент Пуассона; 2) – изменения энтропии при V = const; - изменение энтропии на всем процессе.