Перенос массы Молекулярный механизм переноса массы

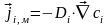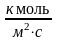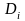, , - коэффициент диффузии.

Для изотермической системы:

.

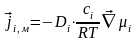Для i-го компонента в случае многокомпонентной системы:

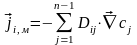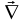, c_i.- градиент концентраций молекул

где 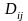- матрица коэффициентов многокомпонентной диффузии.

Для двухкомпонентной системы вырождается в единственный коэффициент бинарной (взаимной) диффузии = 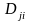и тогда:

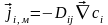. Это соотношение называется первым законом Фика.

Конвективный механизм переноса массы

= .

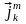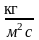
В случае многокомпонентной среды можно рассмотреть поток массы для каждого компонента:

,

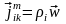Зачастую удобнее использовать поток вещества, а не массы:

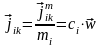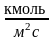, где 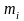- мольная масса компонента i, c_i – мольная концентрация.

Турбулентный механизм переноса массы

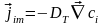
Если учесть, что молекулярная диффузия сохраняется и при турбулентной диффузии можно записать:

= - (D_i+D_т) .

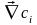Поскольку объем среды, участвующие в турбулентных пульсациях, значительно превышают молекулярные размеры, интенсивность турбулентного переноса массы в пристенной области существенно выше молекулярного:

,

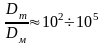При конвективном движении среды поток массы (или вещества) определяются как суммы конвективного и молекулярного переноса, а при турбулентном режиме к ним добавляют и турбулентную составляющую.

Перенос энергии

Полную энергию системы на единицу массы можно записать:

,

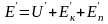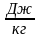
Молекулярный механизм переноса энергии

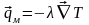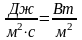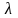Молекулярным механизмом перенос энергии осуществляется в форме тепла. , где - коэффициент молекулярной теплопроводности, 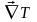- градиент температуры.

переносом кинетической и потенциальной энергии молекул, а также столкновительным переносом:

.

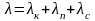Конвективный механизм переноса энергии

Поток энергии, переносимый движущимся макроскопическим объемом за единицу времени через единицу поверхности, можно записать:

.

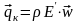Турбулентный механизм переноса энергии

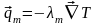. Коэффициент турбулентной теплопроводности

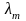
Суммарный поток энергии

.

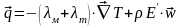Перенос импульса

Молекулярный перенос импульса

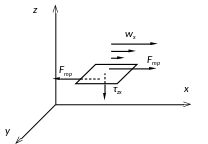
Количество движения по оси x , переносимое вдоль оси z за единицу времени через единицу поверхности можно представить как:

,

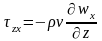где 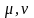- коэффициенты динамической и кинематической молекулярной вязкости. Это уравнение носит название закона Ньютона

Тензор потока импульса за счет молекулярного механизма называется тензором вязких напряжений:

, где 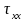, , 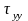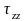- нормальные напряжения, остальные – касательные.

Конвективный перенос импульса

перенос количества движения по оси x за единицу времени через единицу поверхности равен:

.

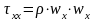Если жидкость движется и по оси y , тогда импульс 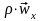будет переноситься и в направлении по оси y:

.

.

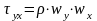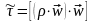Турбулентный перенос импульса

,

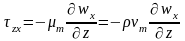где 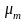, 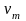- динамический и кинематический коэффициенты турбулентной вязкости.

При конвективном течении жидкости поток импульса складывается из молекулярного и конвективного, а при турбулентном – молекулярного, конвективного и турбулентного:

.

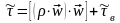Тензор вязких напряжений 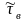, состоит из 9 элементов, которые в нашем случае включают молекулярный и турбулентный перенос импульса:

.

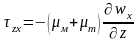И так, рассмотрены уравнения переноса массы, энергии и импульса. Они аналогичны:

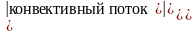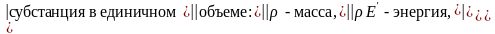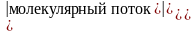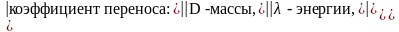= x

= x