Простой пример решения ду в MatLab:
В качестве самого
простого примера приведем решение
следующего уравнения
с начальным условием
и аналитическим решением
.
Возможный формат
вызова процедуры решателя в MatLab:
Снимок экрана, который соответствует численному решению этой задачи в системе MatLab.
Файл-функция, описывающая правую часть уравнения, – текстовый файл с расширением func1.m – содержит всего две строки
Знаком % начинаются
комментарии. Вызываться такая функция
может из другойпрограммы, функции, или,
как в этом случае, из командного окна
Здесь задан временной интервал от Tstart=0 до Tfinal=2 и начальное значение функции StartVector=1. График полученной таким образом функции Y(T) воспроизводится вызовом встроенной функции plot
Следующей строкой
мы кружочками нарисовали на том же
графике точное решение в точках
полученного вектора-столбца T:
В общем случае, процедура ode45 может решать систему уравнений следующего вида:
функция-столбец,
зависящая отвремени и компонент вектора
x.
Заметим, что уравнение (1) можно решить в MatLab и символьно. Приведем часть командного окна, где была вызвана стандартная процедура dsolve
Здесь также использовано начальное условие.
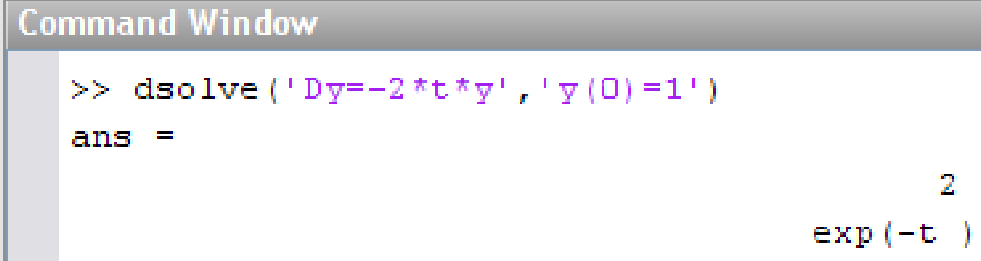
Видим, что с точностью до переобозначения x → t результат совпадает с приведенным выше.
Решение задачи Коши
Задачей Коши называется задача о решении обыкновенного дифференциального уравнения с известными начальными условиями. ВMATLAB имеются три возможности для решения задачи Коши, не считая моделирования в SIMULINK.
Первая из них касается численного решения линейных дифференциальных уравнений с известной правой частью или систем таких уравнений. Оно может быть выполнено с помощью команды lsim (для решения однородных уравнений достаточно команды initial).
Вторая возможность – аналитическое решение линейных и простых нелинейных дифференциальных уравнений с помощью решателя dsolve тулбокса SYMBOLIC.
Пример.
Пусть требуется решить линейное уравнение
второго порядка
В командной строке набираем
MATLAB выдает ответ:
Это означает, что
общее решение данного дифференциального
уравнения имеет вид
Задав начальные
условия
получаем задачу Коши. Для ее решения
набираем
Аналогично решатель dsolve применяют для систем дифференциальных уравнений.
Третья возможность – численное решение нелинейных дифференциальных уравнений с помощью команд типа ode23 и ode45.
Решатели диф. Уравнений в MatLab (solvers)
Для решения систем ОДУ в MatLAB реализованы различные методы. Их реализации названы решателями ОДУ. Решатели реализуют следующие методы решения систем дифференциальных уравнений:
Все решатели (ode45, ode23, ode133, ode15s, ode23s, ode23t, ode23tb ) могут решать системы уравнений явного вида y’ = F(t, y). Решатели ode15s, ode23s, ode23t, ode23tb могут решать уравнения неявного вида F(t, y, y’ )= 0.
ode45 – одношаговые явные методы Рунге-Кутта 4-го и 5-го порядка {начальная пробарешения}. Во многих случаях он дает хорошие результаты;
ode23 – одношаговые явные методы Рунге-Кутта 2-го и 3-го порядка. При умеренной жесткости системы ОДУ и низких требованиях к точности этот метод может дать выигрыш в скорости решения;
ode133 – многошаговый метод Адамса-Башворта-Мултона переменного порядка. Это адаптивный метод, который может обеспечить высокую точность решения;
ode15s – многошаговый метод переменного порядка (от 1-го до 5-го, по умолчанию 5), использующий формулы численного дифференцирования. Это адаптивный метод, егостоит применять, если решатель ode45 не обеспечивает решения;
ode23s – одношаговый метод, использующий модифицированную формулу Розенброка2-го порядка. Может обеспечить высокую скорость вычислений при низкой точности;
ode23t – метод трапеций с интерполяцией. Этот метод дает хорошие результаты прирешении задач, описывающих осцилляторы с почти гармоническим выходным сигналом;
ode23tb – неявный метод Рунге-Кутта в начале решения и метод, использующий формулы обратного дифференцирования 2-го порядка в последующем. При низкой точности этот метод может оказаться более эффективным, чем ode15s.
Пример:
В М-файле с именем pr7.m пишем:
function f=pr7(x,y)
f=cos(x+y)+(3/2)*(x-y);
end
Потом в командном окне вызываем функцию ode113:
ode113(@pr7,[0 20],0) %Метод Адамса: @pr7 – ссылка на М-функцию, [0 20]- интервалы интегрирования,0 - условие: y(0)=0
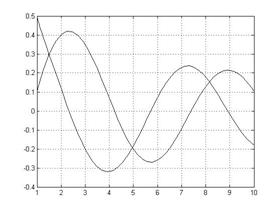
Результатом будет график:
Пример:
Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений:
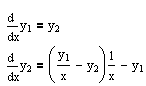
y1(0) = 0.1; y2(0) = 0.5
В М-файле с именем pr8.m пишем:
function dy=pr8(x,y)
dy=zeros(2,1);
dy(1)=y(2);
dy(2)=((y(1)/x)-y(2))*(1/x)-y(1);
end
Потом в командном окне вызываем функцию ode45:
[x,y]=ode45(@pr8,[1 10], [0.1 0.5]);
plot(x,y,'-k')
grid;
Результатом будет график:
