Лабораторна робота № 2. Криптографічна система Лестера Хілла

1. Теоретична частина

При шифруванні заміною (підстановкою) символи шифрованого тексту замінюються символами того ж або іншого алфавіту із заздалегідь встановленим правилом заміни. У шифрі простій заміни кожен символ початкового тексту замінюється символами того ж алфавіту однаково на всьому протязі тексту. Часто шифри простій заміни називають шифрами одноалфавітної підстановки.

Алгебричний метод, який узагальнює афінну систему підставляння Цезаря, формалізований опис якого має такий вигляд:

,

був сформульований Лестером С. Хіллом¹ [7] для визначення n-грам.

Множина цілих чисел , для якої визначені операції додавання, віднімання та множення за модулем m, є прикладом кільця R, тобто алгебричною системою пар елементів. Ця алгебрична система володіє такими властивостями:

• пари елементів кільця R утворюють комутативну групу щодо операції додавання; для неї існують одиничний і зворотний елементи;

• операції множення та додавання задовольняють асоціативному і дистрибутивному законам.

Мультиплікативне зворотне ^-1 елемента  кільця R не завжди може існувати. Наприклад, якщо модуль m = 26, то значення (2^-1)mod 26 і (13^-l)mod 26 не можуть існувати.

Якщо модуль m є простим числом p, то існує зворотна величина будь-якого ненульового елемента t з (при m = p), оскільки значення (1·t)mod m, (2·t)mod m, (3·t)mod m, ..., ((p–1)·t)mod m відрізняються, якщо 1 t  p–1.

Множина , де p – просте число, є прикладом алгебричної системи, яку називають кінцевим полем. Ненульові елементи утворюють мультиплікативну групу.

Множина всіх n-грам з компонентами з кільця утворює векторний простір над кільцем . Кожна n-грама називається вектором. У векторному просторі для векторів визначено операції додавання та віднімання за модулем n, а також скалярне множення вектора на елемент t кільця . Додавання та скалярне множення є операціями, що задовольняють комутативному, асоціативному і дистрибутивному законам. Вектор є лінійною комбінацією векторів , якщо

. (1.5)

Лінійне перетворення є відображенням:

, (1.6)

яке задовольняє умові лінійності

для всіх s, t в і у . Лінійне перетворення може бути представлено матрицею розміром nn такого вигляду

, (1.7)

причому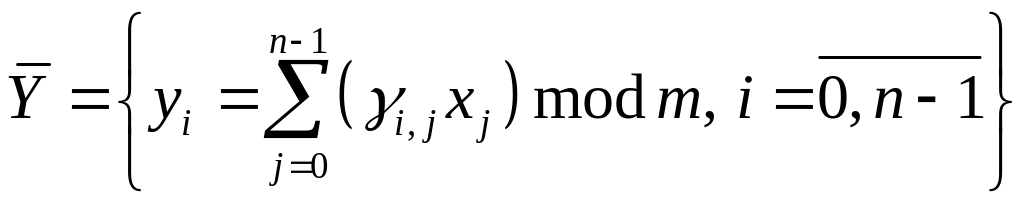

Базисом для векторного простору є набір векторів з , які лінійно незалежні і породжують . Кожен базис для містить n лінійно незалежних векторів. Будь-який набір з n векторів, які лінійно незалежні над називаються базисом.

Нехай є лінійним перетворенням, що описується матрицею (7), причому . Якщо вектори лінійно незалежні над , тоді їх образи лінійно незалежні над тільки в тому випадку, якщо визначник матриці , що позначається як , не ділиться на будь-яке просте p, яке ділить m. Перетворення називається зворотним (або не виродженим) лінійним перетворенням, що має зворотне перетворення :

, (1.8)

де – одинична матриця. Окрім цього, є також лінійним перетворенням. На­приклад, коли m = 26 і матриця перетворення

,

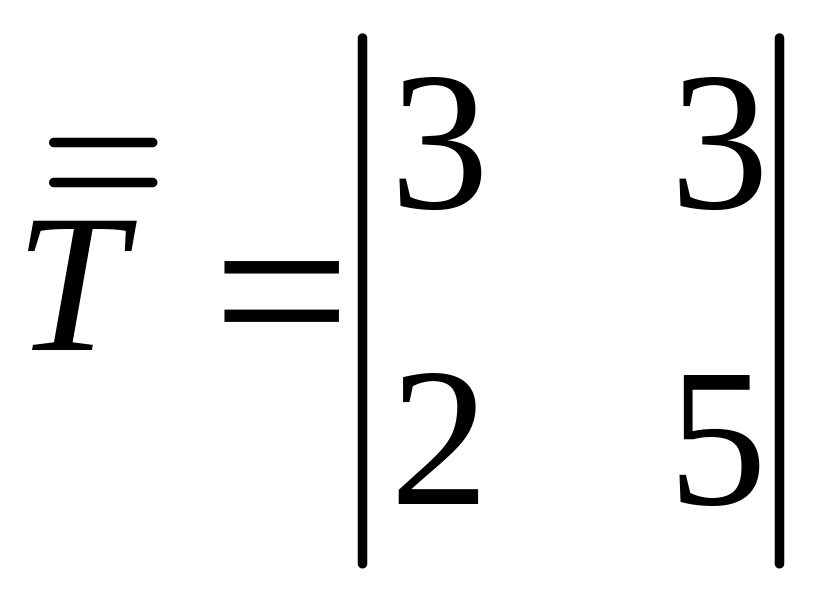то визначник цієї матриці

,

.

Тому існує зворотне перетворення . Неважко переконатися, що задовольняє такому співвідношенню

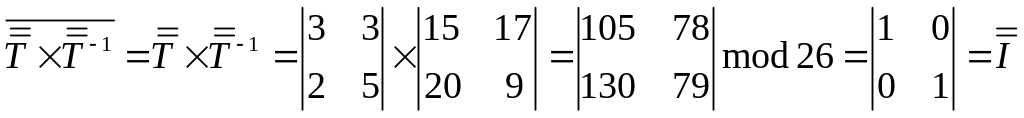
Нехай є лінійним перетворенням на з матрицею . Використовуємо це перетворення для визначення 3-грами підставляння в українському алфавіті за такою таблицею кодів:

0	1	2	3	4	5		0	1	2	3	4	5
а	б	в	г	д	е	0	0	1	2	3	4	5
є	ж	з	и	і	ї	1	6	7	8	9	10	11
й	к	л	м	н	о	2	12	13	14	15	16	17
п	р	с	т	у	ф	3	18	19	20	21	22	23
х	ц	ч	ш	щ	ю	4	24	25	26	27	28	29
я	ь	_	.	,	'	5	30	31	32	33	34	35

Приклад 3. Розглянемо Приклад використання n-грамної криптографічної системи Лестера Хілла стосовно українського алфавіту. Спробуємо зашифрувати вхідний текст "Все йде, все минає, і краю немає." (див. прикл. 1). Вставивши відповідні пропуски, отримаємо таке вхідне повідомлення:

все_йде,_все_минає,_і_краю_немає.

Розбиття цього повідомлення на 3-грами дає такий початковий текст:

все _йд е,_ все _ми нає ,_і _кр аю_ нем ає.

Потім у кожній 3-грамі початкового тексту замінимо кожну букву її числовим еквівалентом згідно з наведеною вище таблицею кодів:

Отримаємо такі 3-грами початкового тексту:

№ п/п	1	2	3	4	5	6	7	8	9	10	11
	все	_йд	е,_	все	_ми	нає	,_і	_кр	аю_	нем	ає.
1	2	32	5	2	32	16	34	32	0	16	0
2	20	12	34	20	15	0	32	13	29	5	6
3	5	4	32	5	9	6	10	19	32	15	33

Перетворення 3-грам початкового тексту в 3-грами заши­фро­ваного тексту здійснюється за таким матричним рівнянням:

.

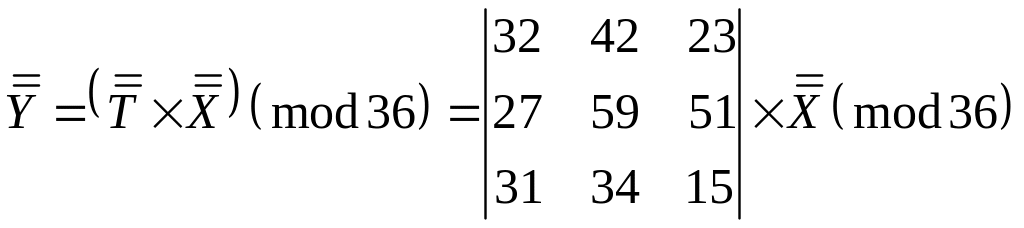Отримуємо:

Шифрування						Матриця
				№	1		2	3	4		5		6		7		8		9		10		11
Т				п/п	все		_йд	е,_	все		_ми		нає		,_і		_кр		аю_		нем		ає.
32	42	23		1	2		32	5	2		32		16		34		32		0		16		0
27	59	51	*	2	20		12	34	20		15		0		32		13		29		5		6		=
31	34	15		3	5		4	32	5		9		6		10		19		32		15		33

					1019	1620	2324	1019	1861	650	2662	2007	1954	1067	1011
				=	1489	1776	3773	1489	2208	738	3316	2600	3343	1492	2037	(mod 36=)
					817	1460	1791	817	1637	586	2292	1719	1466	891	699

						11	0	20	11	25	2	34		27		10		23		3
				=		13	12	29	13	12	18	4		8		31		16		21
						25	20	27	25	17	10	24		27		26		27		15
				п/п		їкц	айс	сфш	їкц	цйо	впі	,дх		шзш		іьч		фнш		гтм
				№		1	2	3	4	5	6	7		8		9		10		11

Замінюючи в 3-грамах зашифрованого тексту числа на відповідні символи, отримуємо 3-граму зашифрованого тексту:

їкц айс сфш їкц цйо впі ,дх шзш іьч фнш гтм

При дешифруванні цього зашифрованого тексту застосовується зво­рот­ний порядок дій. Перетворення 3-грами заши­фро­ваного тексту в 3-грами початкового тексту здійснюється за таким матричним рівнянням:

.

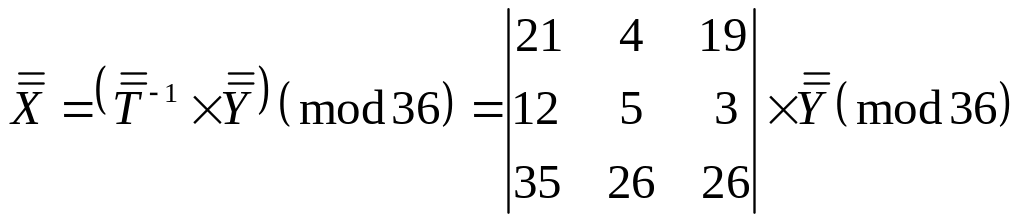Отримуємо:

Дешифрування					Матриця
				№	1	2	3	4	5	6	7	8	9	10	11
Т-1				п/п	їкц	айс	сфш	їкц	цйо	впі	,дх	шзш	іьч	фнш	гтм
21	4	19		1	11	0	20	11	25	2	34	27	10	23	3
12	5	3	*	2	13	12	29	13	12	18	4	8	31	16	21	=
35	26	26		3	25	20	27	25	17	10	24	27	26	27	15

					758	428	1049	758	896	304	1186	1112	828	1060	432
				=	272	120	466	272	411	144	500	445	353	437	186	(mod 36=)
					1373	832	2156	1373	1629	798	1918	1855	1832	1923	1041

						2	32	5	2	32	16	34		32		0		16		0
				=		20	12	34	20	15	0	32		13		29		5		6
						5	4	32	5	9	6	10		19		32		15		33
				п/п		все	_йд	е,_	все	_ми	нає	,_і		_кр		аю_		нем		ає.
				№		1	2	3	4	5	6	7		8		9		10		11

У розглянутому прикладі матриці перетворення мали розмір 33 і шифрувалися 3-грами (парами) букв. Хоча буква е може бути зашифрована по-різному в різних парах початкового повідомлення, одна і та ж пара, наприклад все, шифруватимемо завжди однаково впродовж всього початкового тексту. Система шифрування Хілла є одноалфавітною в широкому сенсі цього слова.