Завдання 15

Пропозиція грошей здійснюється за формулою М=150+5і швидкість їх обігу дорівнює 25 обертам за період на протязі якого створюється реальний дохід в розмірі 2900 од. Реальний попит на гроші як майно характеризується формулою 48-2і. Визначте рівноважну ставку процента.

Методичні рекомендації

Слід розрізняти дискреційну та автоматичну фіскальну політику. В основі дискреційної політики лежить цілеспрямоване застосування державних закупівель і чистих податків. Зазначені фіскальні засоби впливають на дохід мультиплікативно. Але слід брати до уваги, що в умовах змішаної економіки закритого типу виникає складний мультиплікатор видатків, який, крім заощаджень, враховує ще один канал вилучень — податки у формі чистих податків (Т). При цьому вилучення у формі податків відбуваються автоматично в разі зміни доходу як податкової бази згідно з граничним коефіцієнтом податків (t). У разі врахування заощаджень і автоматичних чистих податків вилучення збільшуються і становлять величину 1 - с • (1 - t). Звідси випливає формула складного мультиплікатора видатків:

або

Мультиплікатор податків завжди менший мультиплікатора видатків пропорційно граничній схильності до споживання. Це дає підстави перейти до мультиплікатора податків (m_t):

Використовуючи наведені мультиплікатори, можна обчислити вплив на дохід державних закупівель або чистих податків, які змінюються дискреційнo, тобто за рахунок зміни податкових ставок або рівня трансфертів. Державні закупівлі належать до автономних видатків і впливають на реальний ВВП безпосередньо. Якщо ΔG = ΔAЕ, то приріст реального ВВП визначається так:

ΔY=ΔG*m_e

Особливість чистих податків, які змінюються дискреційне, поляґає в тому, що вони не є компонентом автономних видатків, а впливають на ВВП опосередковано через автономне споживання. Між чистими податками і автономним споживанням існує обернений зв'язок: ΔT*с=-ΔС. Якщо ΔT• с =- ΔАE=-ΔС, то вплив чистих податків на реальний ВВП можна визначити за формулою:

ΔY=-ΔT*c*m_e=-ΔT*m_t

Порівнюючи дві останні формули, слід звернути увагу на знаки. Вони свідчать про те, що між G і Y існує пряма залежність, а між Т і Y— обернена.

В умовах інфляції вплив державних закупівель або чистих податків на реальний ВВП визначається через їх вплив на номінальний ВВП. Якщо ΔGⁿ =ΔAEⁿ або ΔTⁿ =-ΔAEⁿ , то приріст реального ВВП визначається за такими формулами:

Крім автономного застосування фіскальних засобів держава може застосовувати їх одночасно. Тоді зміна доходу визначається за формулою (при стабільних цінах):

ΔY=ΔG*m_e-ΔT*m_t або ΔY=m_e(ΔG-ΔT*c)

Підсумковий результат у цьому варіанті залежить від співвідношення між зміною G і Т з урахуванням того, що мультиплікатор видатків є вищим від мультиплікатора податків. Але якщо державні закупівлі й чисті податки змінюються за умов збалансованого бюджету, тобто коли ΔG = ΔТ, то результатом такої політики буде певний приріст доходу, оскільки ΔG > ΔТ*с .

Фіскальна політика в умовах збалансованого бюджету породжує ще одну категорію — мультиплікатор збалансованого бюджету (m_b). Він показує, на скільки грошових одиниць змінюється дохід у разі зміни державного бюджету на грошову одиницю тобто відображає співвідношення між зміною доходу і зміною бюджету (ΔВ):

m_b= ΔY/ ΔВ

При визначенні мультиплікатора збалансованого бюджету слід враховувати податки, які перетворюють простий мультиплікатор видатків у складний: m_е=1/s+c*t. За цих умов ΔY= т_е(ΔG-c*ΔT). Оскільки ΔТ=ΔG=ΔВ, то мультиплікатор збалансованого бюджету можна визначити так:

Після скорочення і певних перетворень останньої формули дістанемо формулу мультиплікатора збалансованого бюджету:

m_b=m_e(1-c) або m_b=m_e-m_t

У розгорнутому вигляді це можна записати так:

Отже, мультиплікатор збалансованого бюджету завжди менший одиниці.

Досі ми розглядали дискреційну фіскальну політику, в межах якої на основі державних рішень змінюються державні закупівлі та чисті податки. Тепер перейдемо до автоматичної фіскальної політики, в основі якої лежить автоматична зміна чистих подат­ків, тобто їх зміна без прямої участі держави.

Чисті податки, які залежать від доходу, називають автоматичними. Це означає, що величина їх вилучень до бюджету змінюється в автоматичному режимі згідно зі зміною доходу як подат­кової бази економіки в цілому і граничним коефіцієнтом податків: ΔТ=t*ΔY.

Виникає питання — як визначається ефект гальмування динаміки виробництва з боку автоматичних чистих податків? Величина цього гальмування залежить від впливу автоматичних чистих податків на мультиплікатор.

Як ми знаємо, мультиплікатор видатків, що враховує вилучення, лише у формі заощаджень, визначається за формулою:m_e=1/1-c. Але якщо вилучення доповнити автоматичними чистими податками, то виникає складний мультиплікатор:m_e=1/s+c*t. Оскільки s+c*t>s, то це означає, що мультиплікатор з урахуванням автоматичних податкових вилучень нижчий ніж за їх відсутності. Зазначене адекватно зменшує мультиплікативну зміну доходу.

Узагальнюючи попередній аналіз, ефект гальмування динаміки виробництва (ΔУ), викликаного автоматичними чистими податками, можна визначити таким чином (при стабільних цінах):

.

Досі фіскальна політика розглядалася без урахування її бюджетних наслідків. Тепер слід урахувати бюджетну функцію фіскальної політики, тобто визначити, з якими наслідками для державного бюджету фіскальна політика виконує стабілізаційну функцію в економіці.

Бюджетна діяльність держави має бути різною залежно, від фази економічного циклу. Так, під час скорочення виробництва ефективною (доцільною) є стимулювальна фіскальна політика, яка викликає бюджетний дефіцит або збільшує його рівень. Під час інфляційного зростання ефективною є стримуюча фіскальна політика, яка викликає скорочення бюджетного дефіциту або виникнення бюджетного профіциту.

Проте на стан державного бюджету впливають також циклічні коливання в економіці. Під час спаду виробництва автоматично скорочуються податкові надходження в бюджет, а за його зростання — вони збільшуються. Тому, щоб визначити ефективність фіскальної політики, треба розмежувати вплив на державний бюджет фіскальних заходів і циклічних коливань.

Стан державного бюджету визначається з допомогою бюджетного сальдо (BS), яке можна обчислити як різницю між чистими податками і державними закупівлями: BS=T-G. Слід розрізняти фактичне, потенційне і циклічне бюджетне сальдо.

Фактичне бюджетне сальдо характеризує стан державного бюджету в умовах фактичного рівня зайнятості і тому обчислюється на базі фактичного доходу за формулою BS = Y • t - G, де t- середній коефіцієнт податків, a Y*t — фактичні податкові надходження до бюджету. Таке бюджетне сальдо відображає вплив на державний бюджет як фіскальної політики, так і циклічних коливань.

Вплив циклічних коливань на стан державного бюджету можна нейтралізувати, якщо як податкову базу використати потенційний дохід (Yp). Завдяки цьому можна обчислити потенційне бюджетне сальдо за формулою BS_p =Y_р*t-G . Воно показує, яким могло б бути бюджетне сальдо, коли б економіка функціонувала в умовах повної зайнятості.

Якщо економіка перебуває в умовах неповної зайнятості, то державний бюджет втрачає певну величину доходів. Ці втрати відображає циклічне бюджетне сальдо, яке обчислюється за формулою BS_с= BS - BS_р.

Основними параметрами грошового ринку є грошова пропозиція і грошовий попит. Вони являють собою реальну грошову масу і обчислюються на основі ділення номінальної грошової маси (М) на ціни за формулами: пропозиція — М^s=(M/P)^s, попит — M^d = (M/P)^d. Крім того, важливим параметром грошового ринку є ціна грошей, тобто відсоткова ставка.

Грошова пропозиція складається з різних форм грошових активів. Залежно від рівня ліквідності всі вони об'єднуються зростаючим підсумком в окремі грошові агрегати:

МО = готівкові гроші (гроші поза банками);

М1= МО + поточні депозити + кошти на розрахункових рахунках;

М2 = Ml + строкові депозити;

МЗ = М2 + кошти клієнтів за трастовими операціями банків.

Грошова пропозиція не залежить від відсоткової ставки, а може змінюватися Національним банком згідно з цілями монетарної політики. Тому в графічній моделі грошової пропозиції її крива набирає вигляду вертикальної лінії.

Складнішою категорією є грошовий попит, який складається з двох елементів: попит на гроші для угод (трансакційний попит) — М^d1 і попит на гроші як активи (спекулятивний попит) — М^d2.

Попит на гроші для угод випливає з їхньої функції платіжного засобу. Тому його величина прямо залежить від реального доходу. Звідси випливає функція попиту на гроші для угод:

М^d1=k*Y

де k — коефіцієнт чутливості грошового попиту до зміни доходу, який показує, на скільки грошових одиниць змінюється грошовий попит при зміні доходу на одну грошову одиницю.

Отже, попит на гроші для угод теж не залежить від відсоткової ставки. Тому в графічній моделі крива цього попиту набирає вигляду вертикальної лінії.

Попит на гроші як активи випливає з їх функції засобу зберігання вартості. Щоб зрозуміти, від чого залежить цей попит, слід, розглянути, як приклад, два альтернативні варіанти зберігання вартості:

1) у формі грошей,

2) у формі облігацій, які належать до не грошових активів.

Порівнюючи ці два види активів, треба враховувати їхні переваги й недоліки. Перевагою грошей як засобу зберігання вартості є висока ліквідність, але вони не приносять дохід їх власникам .Переваги облігацій полягають у тому, що вони приносять дохід у формі відсотків, але мають низьку ліквідність.

Чим вища відсоткова ставка, тим більші втрати від зберігання вартості у формі грошей, тим менший попит на гроші і більший - на облігації. Це свідчить про те, що попит на гроші як активи перебуває в оберненій залежності від відсоткової ставки. Тому на графіку крива цього попиту набирає вигляду від'ємно похилої лінії. Це дає підстави визначити функцію попиту на гроші як активи за такою формулою:

М^d2=-h*n,

n - коефіцієнт чутливості грошового попиту до зміни від­соткової ставки, який показує, на скільки грошових одиниць змінюється грошовий попит при зміні відсоткової ставки на один пункт.

Отже, сукупний попит — це реальна грошова маса, яка не­обхідна економічним суб'єктам для оплати угод та як активи. Підсумовуючи попередній аналіз, функцію грошового попиту можна записати так:

М^d=L(Y,n)=k*Y-h*n.

Звідси зміна грошового попиту визначається за формулою:

ΔM^d=k*ΔY-h*Δn.

На рисунку 1.3 похила лінія М^d — це крива сукупного грошового попиту. Її особливість полягає в тому, що вона зміщена вправо від вертикальної осі на певну відстань (див. стрілку). Таке зміщення відображає величину попиту на гроші для угод, який не залежить від відсоткової ставки. Завдяки цьому крива М^d набуває здатності відображати весь грошовий попит. Вертикальна лінія М₁^s— це початкова крива грошової пропозиції. Перетин кривих М ^d і M₁^s у точці Т₁ свідчить про початкову рівновагу на грошовому ринку за рівноважної відсоткової ставки на рівні n₁.

Якщо припустити, що Національний банк збільшив грошову пропозицію, то її крива зміститься в положення М^s₂ . За даної відсоткової ставки рівновага порушується: М^s₂ >М^d. Але ринок тяжіє до рівноваги. Механізм відновлення рівноваги буде таким:

Рис.1.3. Крива сукупного грошового попиту

1) перевищення пропозиції над попитом викликає появу над­лишкових грошей, які спрямовуються на придбання облігацій;

2) надлишкові гроші збільшують попит на облігації, що під­вищує їх ціну;

3) зростання цін на облігації викликає зниження відсоткової ставки, що випливає з її формули:

n = (відсотковий дохід / ціна облігації) * 100,

де відсотковий дохід є фіксованою величиною. Тому в разі зростання цін на облігації відсоткова ставка падає. На рисунку вона зменшиться до n₂, що збільшить грошовий попит до рівня грошової пропозиції і врівноважить грошовий ринок.

Національний банк регулює грошову пропозицію через комерційні банки. Щоб зрозуміти роль комерційних банків у формуванні грошової пропозиції, слід враховувати, що вони виконують дві основні функції: 1) залучення грошей на депозит, 2) надання позик та здійснення інвестицій.

Кошти, залучені на депозит, формують загальні резерви банківської системи (TR), які розподіляються на дві частини за формулою: TR = LR + ER.

LR — це обов'язкові резерви. Їх величина визначається згідно з нормою обов'язкового резервування (Іr), рівень якої регламентується Національним банком відносно депозитів (D). Звідси обов'язкові резерви визначаються за формулою: LR = Іr • D;

ER — це надлишкові резерви, які обчислюються як різниця між загальними резервами (залученими депозитами) й обов'язковими резервами: ER=TR-LR або ER = D - LR. Надлишкові резерви використовуються для проведення комерційними банками активних операцій: надання позик та здійснення інвестицій.

Здатність банківської системи примножувати початковий приріст депозитів визначається депозитним мультиплікатором (m_d). Він перебуває в оберненій залежності від резервної норми і визначається за формулою:

,

де rr - резервна норма (загальна), яка визначається за формулою:

rr= (LR + ER)/ D

Приріст депозитів збільшує грошову пропозицію. Проте зв'язок між ними може бути різним. Якщо приріст депозитів банківської системи започатковується за рахунок грошової емісії (дисконтних позик Національного банку або продажу йому державних цінних паперів), то грошова пропозиція збільшується адекватно збільшенню депозитів: ΔM^s = ΔD = . Але приріст депозитів банківської системи може забезпечуватися і приватним сектором (домогосподарства, підприємства). Найбільш типове джерело початкового приросту депозитів — вклади населення. У цьому разі депозити збільшуються за звичайною формулою (ΔD= ). Проте приріст грошової пропозиції (новостворені гроші) буде меншим на величину початкового приросту депозитів, оскільки його було забезпечено за рахунок перетворення наявної в обігу готівки в безготівкові гроші: ΔM ^s =ΔD- . Якщо замість ΔD підставити , то приріст грошової пропозиції, викликаний вкладами приватного сектора, визначиться за формулою: ΔM ^s =ΔD (m_d-1).

Досі ми розглядали спрощену модель грошової пропозиції, яка складається лише із банківських депозитів, тобто M^s =D. Насправді грошова пропозиція, крім банківських депозитів, включає також готівку:

М^s =CU+D,

де CU — готівкові гроші.

Грошово-кредитне регулювання економіки здійснює Національний банк з допомогою монетарної політики. Теоретичною базою монетарної політики слугує монетаристська теорія, в основі якої лежить кількісне рівняння:

М*V =P*Y.

Згідно з монетаристською теорією, швидкість обертання грошей (V) є стабільною, а можливі її зміни можна легко передбачити. За цих умов держава, регулюючи грошову масу (М), може цілеспрямовано впливати на номінальний ВВП, тобто на добуток P*Y. Спираючись на це положення, М. Фрідмен, який є засновником монетаристської теорії, запропонував установити «монетарне правило», за яким грошова маса має щорічно збільшуватися такими самими темпами, що й темпи приросту реального ВВП.

Пріоритетною функцією монетарної політики є антиінфляційна. Згідно з кількісним рівнянням (P*Y=M*V) ціна є функцією трьох чинників: P=F(M, V, Y). Головним серед них є грошова маса (M), яку контролює Національний банк. В умовах економічного зростання і невисокої інфляції він, регулюючи грошову масу і прогнозуючи Y і V, дістає можливість забезпечувати досягнення цільового рівня інфляції.

Досі розглядалися умови рівноваги окремо на товарному та грошовому ринках. Насправді економічна рівновага — це рівновага на обох ринках одночасно. Аналітичним засобом поєднання двох ринків на умовах рівноваги є модель IS—LM. Двома її складовими є крива IS (інвестиції — заощадження) та крива LM (ліквідність — гроші).

Крива IS відображає зв'язок між реальною відсотковою ставкою (r) і доходом (Y) в умовах рівноваги на товарному ринку. Крива LM відображає зв'язок між Y і r в умовах рівноваги на грошовому ринку. Оскільки відсоткова ставка впливає на товарний ринок (через інвестиційний попит) і одночасно є елементом грошового ринку, то завдяки цьому вона пов'язує між собою обидва ринки. Модель IS—LM пристосована для умов, якщо ціни стабільні. Тому n = r. Ми будемо спиратися на реальну відсоткову ставку, оскільки в моделі IS—LM вона є чинником інвестицій.

Криву IS можна побудувати на основі синтезу моделі «кейнсіанський хрест» і графіка інвестиційного попиту (див. рис. 1.4).

а) «кейнсіанський хрест»

E

E1

T1

E2

T2

Y

Y2 Y1

r r

r 2 T2 r2 T2

I

Y

r

IS

Y

1 T1 r1 T1

Y2 Y1 Y2 Y1

б) крива ІS в) крива інвестиційного попиту

Рис.1.4. Побудова кривої IS

Припустимо, що відсоткова ставка зросла від г₁, до г₂. Згідно з інвестиційною функцією (І=І-Ь*r), інвестиції скоротяться від І₁ до І₂ (графік інвестиційного попиту). Це викличе зменшення сукупних видатків з Е₁ до Е₂ і доходу від Y₁ до Y₂ («кейнсіанський хрест»). Крива IS підсумовує зазначені зміни. Вона набирає вигляду від’ємної похилої лінії і свідчить про обернену залежність між відсотковою ставкою і доходом.

Виведемо алгебраїчну модель кривої IS, спираючись на такі рівняння:

Y=E; Y=C+I+G; C= +c(Y-T); I= -b*r; G= .

Об'єднаймо ці рівняння в одне, в якому замість c(Y-T) підставимо c(l-t) Y:

Y= + + +c(l-t)*Y-b*r.

Перенесемо Y із правої частини рівняння в ліву:

Y-c(l-t)*Y= + + -b*r.

Розв'язавши рівняння відносно Y, отримаємо:

.

Для спрощення рівняння суму автономних видатків + + позначимо як АЕ і врахуємо, що вираз 1/1-с(1-t) є мультиплікатором видатків (m_e). Звідси випливає функція кривої IS:

Y=m_e(AE-b*r)

Тепер перейдемо до кривої LM, яку можна побудувати на основі синтезу моделі «кейнсіанський хрест» та графіка грошового ринку (див. рис.).

Припустимо, що дохід збільшився від Y₁, до Y₂ («кейнсіанський хрест»). Це збільшує попит на гроші, що переміщує його криву вправо і підвищує відсоткову ставку від г₁ до r₂ . Крива LM підсумовує зазначені зміни. Вона набирає вигляду додатної похилої лінії і свідчить, що між доходом і відсотковою ставкою існує пряма залежність.

Виведемо алгебраїчну модель кривої LM на основі рівняння рівноваги на грошовому ринку. Пригадаймо, що функція грошового попиту визначається за формулою:

М^d = k • Y - h • r.

Тоді рівновага на грошовому ринку матиме такий вигляд:

М^s = k • Y - h • r. Розв'язавши це рівняння відносно r, дістанемо функцію кривої LM:

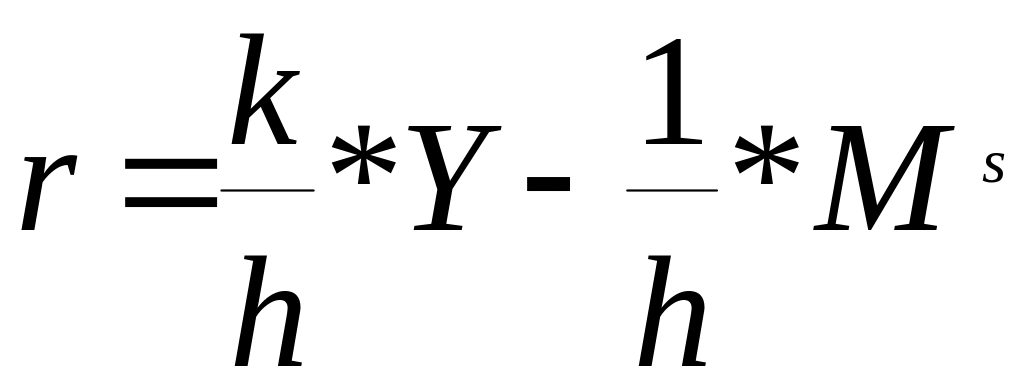
а) «кейнсіанський хрест»

r

Е2

T2

T1

Y1 Y2 Y

LM

r

М^s

T2 r2 T2

r 2

T1 r1 М2^d

r1 М1^d

Y1 Y2 Y Y

Т₁

Рис.1.5. Побудова кривої LM

Тепер можемо поєднати на одному графіку криві IS та LM

r IS LM IS2 LM

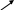
r 0 r2

IS2

r2 IS1

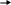Y0 Y Y1 Y2 Y

Рис.1.6 Рівновага в моделі IS — LM Рис.1.7 Стимулювальна фіскальна політика

r LM1

r1 LM2

r2

IS

Y₁ Y₂ Y

Рис.1.8. Стимулювальна монетарна політика

Економічна рівновага в моделі IS—LM — це точка, в якій перетинаються обидві криві. Ця точка визначає відсоткову ставку (r_о) і дохід (Y_о), які відповідають умовам рівноваги як на товарному, так і на грошовому ринках. У точці рівноваги фактичні видатки дорівнюють запланованим, а грошовий попит — грошовій пропозиції.

Модель IS—LM використовують для пояснення впливу фіскальної і монетарної політики на дохід у короткостроковому періоді з припущенням, що ціни є стабільними. При цьому треба брати до уваги, що в даній моделі до екзогенних змінних належать державні закупівлі, чисті податки і грошова пропозиція, а до ендогенних — дохід і відсоткова ставка. Це визначає характер впливу фіскальної та монетарної політики на криві IS і LM.

У разі застосування стимулювальної фіскальної політики відбувається збільшення доходу і зростання відсоткової ставки, що з урахуванням ефекту витіснення переміщує криву IS вгору. Із застосуванням стимулювальної монетарної політики відбувається зниження відсоткової ставки і збільшення доходу, що переміщує криву LM вниз. Модель IS—LM пояснює не лише автономний вплив фіскальної та монетарної політики на економіку. Оскільки об'єктами їх впливу є однакові ендогенні змінні (Y, r), то завдяки цьому модель IS—LM дає можливість узгоджувати між собою дію окремих складових макроекономічної політики.

Література до теми 8: [1; с.143-170], [2; с.290-314, 450-471], [3; с.104-116], [4; с.402-434], [6; с.159-175], [6; с.144-156].

Література до теми 9: [1; с.171-274], [2; с.315-392], [3; с.117-125], [4; с.182-202, 366-401], [5; с.176-192], [6; с.157-173].