7. Розрахунок та конструювання другорядної балки.

Другорядну балку попередньо приймаємо, як відзначено в п. 5.1, розмірами перерізу b_sb×h_sb=200×350мм. Другорядна балка марки ДБ_м-1 працює як п’яти- пролітна нерозрізна балка з крайніми опорами на цегляних стінах і проміжними опорами на головних балках. Окремий тип другорядних балок марки ДБ_м-2 обпирається на цегляні стіни і колони (рис. 7.1).

7.1. Обчислення розрахункових прольотів другорядної балки.

Для обчислення розрахункових прольотів другорядної балки приймемо до уваги попередньо прийняті розміри перерізу головної балкиb_mb×h_mb=300×800мм (п. 5.1) і розглянемо розріз 2-2 на плані перекриття (рис. 7.1). Крайні шарнірні опори на стінах розташовуємо посередині опорних ділянок с_sb=250мм, а проміжні опори – по гранях головних балок.

Таким чином, розрахункові прольоти другорядної балки обчислюємо за формулами:

– крайній:

;

– середній:

.

7.2. Обчислення навантаження.

Другорядну балку розраховують як багатопролітну нерозрізну балку з рівномірно розподіленим погонним навантаження. Навантаження на балку складається з постійного навантаження від власної ваги конструкції підлоги, плити перекриття і власної ваги ребра другорядної балки, а також зі змінного (корисного) навантаження на перекриття.

Лінійне (погонне) розрахункове граничне навантаження на другорядну балку при кроці балок а_sb=2 м:

1) постійні навантаження:

– від власної ваги конструкції підлоги і монолітної плити перекриття, якщо поверхневе навантаження за табл. 5.3 g_tab=3,762кН/м²:

g_d=g_tabа_sb=3,762·2=7,542кН/м;

– навантаження від власної ваги ребра другорядної балки:

g_sb=b_sb(h_sb–h_pl)ργ_fm=0,15∙(0,35–0,08)∙2500∙(0,01)∙1,1=1,11кН/м;

де ρ =2500кг/м³–густина залізобетону; в кН/м3

γ_fm=1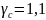,1 – коефіцієнт надійності за навантаженням (табл. 5.1 Норм [1]);

– сумарне постійне навантаження:

g=g_d+g_sb=7,542+1,11=8,652кН/м;

2) змінне навантаження, якщо поверхневе граничне навантаження за табл. 5.3 v_tab=8,4кН/м²:

v=v_tab=8,4·2,2=18,48кН/м;

3) повне розрахункове граничне навантаження:

q=g+v=8,652+18,48=27,132кН/м

7.3. Статичний розрахунок другорядної балки.

П’яти -пролітну нерозрізну другорядну балку розглядають завантаженою погонним постійним навантаженням по всіх прольотах і всіма можливими варіантами (схемами) завантажень окремих прольотів змінним навантаженням. Розрахункова схема балки за однією із схем навантаження наведена на рис. 6.3а. При різноманітних схемах завантаження нерозрізної балки змінним навантаженням в її перерізах виникають найбільші і найменші внутрішні зусилля – моменти М та поперечні сили Q, а епюри цих зусиль носять огинаючий характер (рис. 6.3б,в). При цьому що більше співвідношення змінного навантаження до постійного v/g, тим більшими виникають від’ємні прольотні моменти. Характер епюр і величини внутрішніх зусиль обчислюють з урахуванням пластичної роботи залізобетону.

Таким чином, розрахункові граничній моменти в п’яти-пролітній балці:

– в крайніх прольотах:

;

– на першій від краю опорі:

;

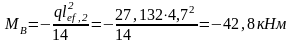– в середніх прольотах та на середніх опорах:

;

Від’ємні пролітні моменти на віддалі 0,2l_ef,2 від опори В вправо та . від опори С вліво. обчислюємо за рекомендаціями [7], рис. 6.91, табл. 6.29 за формулою, зокрема:

М₆ =β₆ql_ef,2²,

де β₆ – від’ємний коефіцієнт за табл. 6.29 [7] залежно від співвідношення змінного навантаження до постійногоv/g. В нашому випадку,

.

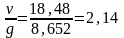При цьому за табл. 6.29 [7] коефіцієнт β₆ =–0,031,а значення від’ємного пролітного моменту, якщо q=27,132кН/м :

М₆ =β₆ql_ef,2²= – 0,031·27,132·4,7² = – 18,58кНм.

Поперечні сили, що виникають в балці:

• на крайній опорі

Q_A=0,4q(l_ef,1–0,5c_sb)=0,4·27,132(4,525–0,5·0,25)=47,75кН;

• на другій від краю опорі зліва:

Q_B,left=0,6ql_ef,1=0,6·27,132·4,525=27,66кН;

– на другій від краю опорі справа:

Q_B,right=0,5ql_ef,2=0,5·27,132·4,7=63,76кН.

Огинаючі епюри моментів М (кНм) і поперечних сил Q (кН) подані на рис. 7.3.