75 Последовательные реакции первого порядка

Последовательными называются такие реакции, которые протекают через ряд последовательных стадий по схеме:

.

Здесь каждой буквой обозначается отдельная стадия процесса. Реакции подобного типа широко распространены в природе. В общем случае число ступеней в последовательных реакциях может быть и больше трёх, причём каждая из ступеней может быть не мономолекулярной, а более сложной. К реакциям этого типа относятся, в частности, реакции гидролиза сложных эфиров дикарбоновых кислот, или сложных эфиров гликолей, или дигалогенпроизводных и т.д.

Примером последовательных реакций может служить гидролиз трисахарида рафинозы, который происходит через стадии образования дисахарида, а последний образует уже моносахариды:

1)

2)

Расчёт кинетики последовательных реакций можно произвести, если принять, что в начальный момент времени есть только вещество А. Применим к этой системе закон действующих масс и принцип независимости химических реакций:

с начальными условиями

Р

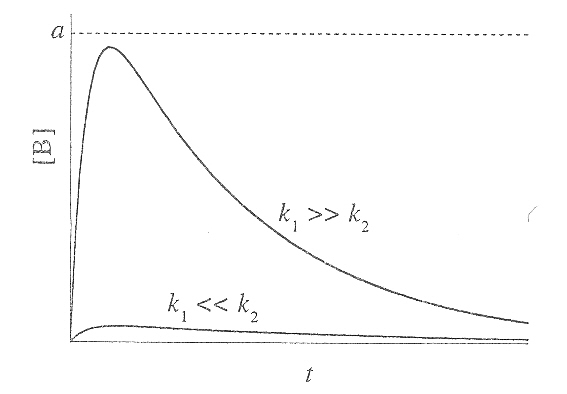
Рис. 15.2. Зависимость концентрации промежуточного продукта от времени в системе двух последовательных реакций при различных соотношениях констант скорости первой и второй стадии.

ешение этой системы даёт концентрации

веществ:

Концентрация промежуточного вещества достигает максимума при

Величина этого максимума определяется отношением констант . Если оно мало, то промежуточный продукт быстро накапливается и медленно расходуется. Если же оно велико, т.е. , то промежуточный продукт не успевает накапливаться и его концентрация в любой момент времени мала (рис. 15.2.).

76 Обратимые реакции первого порядка

Обратимыми называются такие реакции, скорость которых равна разности между скоростями прямой и обратной реакции:

.

Примером обратимой реакции может служить реакция образования сложного эфира

В этом случае скорость прямой реакции с течением времени убывает, а скорость обратной реакции возрастает до тех пор, пока обе скорости не выравняются и не наступит так называемое состояние динамического равновесия.

Для обратимых реакций первого порядка:

Закон действующих масс записывается следующим образом:

Если начальные концентрации веществ А и В обозначить, соответственно, a и b и ввести степень превращения x то кинетическое уравнение приобретает вид:

Решение этого уравнения можно выразить через степень превращения, соответствующую достижению равновесия:

или

г

де х_∞ определяется условием равенства скоростей прямой и обратной реакций:

откуда следует:

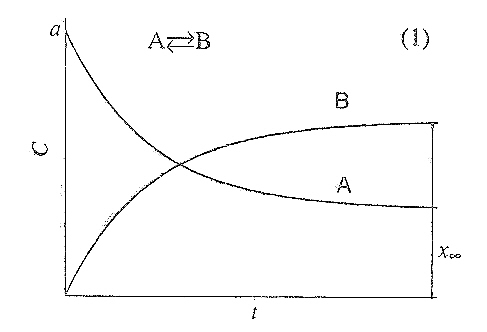
Рис. 15.3. Зависимость концентраций реагента и продукта от времени для обратимой реакции первого порядка.

При наступает равновесие

которое, характеризуется константой:

Кинетические кривые для обратимых реакций 1-го порядка приведены на рис. 15.3.