Тема № 5.Составление уравнения прямой.
1.Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.
уравнение
этой прямой в отрезках:
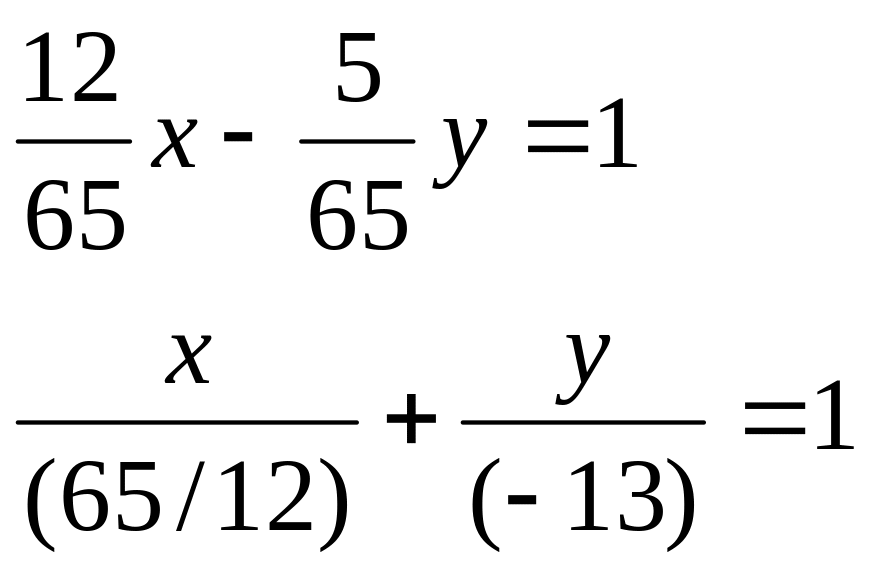
уравнение этой прямой с угловым коэффициентом: (делим на 5)
нормальное уравнение прямой:
;
cos
= 12/13; sin
= -5/13; p
= 5.
Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.
2. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2.
Уравнение
прямой имеет вид:
,
a
= b
= 1; ab/2
= 8; a
= 4; -4.
a = -4 не подходит по условию задачи.
Итого:
или х + у – 4 = 0.
3. Составить уравнение прямой, проходящей через точку а(-2, -3) и начало координат.
Уравнение
прямой имеет вид:
,
где х1
= у1
= 0; x2
= -2; y2
= -3.
4.Определить угол между прямыми: y = -3x + 7; y = 2x + 1.
k1
= -3; k2
= 2 tg
=
;
= /4.
5.Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.
Находим: k1 = 3/5, k2 = -5/3, k1k2 = -1, следовательно, прямые перпендикулярны.
6. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.
Находим
уравнение стороны АВ:
;
4x
= 6y
– 6;
2x
– 3y
+ 3 = 0;
Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.
k
=
.
Тогда y
=
.
Т.к. высота проходит через точку С, то
ее координаты удовлетворяют данному
уравнению:
откуда
b
= 17. Итого:
.
Ответ: 3x + 2y – 34 = 0.
Тема № 6.Определение параллельности и перпендикулярности прямых.
Пусть даны две прямые на плоскости, заданные уравнениями:
и
,
где
-угловые
коэффициенты, равные тангенсам углов
наклона прямых к положительному
направлению оси
.
Если прямые
параллельны, то их углы с осью
равны, поэтому и их угловые коэффициенты
равны, т.е. условием параллельности двух
прямых является равенство их угловых
коэффициентов:
.
Если прямые
перпендикулярны, то углы, под которыми
они пересекают ось
,
различаются на
,
следовательно, условие перпендикулярности
можно записать в виде:
1. Треугольник задан вершинами: А(-6;-2), В(4;8), С(2;-8).
Найти:
1.Уравнение прямой ВN, параллельной стороне АС.
2.Уравнение медианы СD.
3.Уравнение высоты АЕ.
4.Угол
.
Решение:
Составим уравнение прямой АС, используя уравнение прямой, проходящей через две точки
.
АС:
.
Запишем его в виде
уравнения прямой с угловым коэффициентом:
.Т.к.
прямые АС и ВN параллельны, их угловые
коэффициенты равны (
).Воспользуемся
уравнением прямой, проходящей через
заданную точку в данном направлении
ВN:
,
или
.
Ответ: .
2. Найдем
координаты точки D как середины отрезка
АВ:
,
.
Воспользуемся
уравнением прямой, проходящей через
две заданные точки:
.
.
СD:
.
Ответ: .
3. Составим
уравнение прямой ВС, используя уравнение
прямой, проходящей через две точки
.
,
ВС:
.
Запишем его в виде
уравнения с угловым коэффициентом:
Т.к.
АЕ - высота треугольника, следовательно
.
Из условия
перпендикулярности прямых:
,
.
Используем уравнением прямой, проходящей через заданную точку в данном направлении
АЕ:
,
или
.
Ответ: .
4. Составим
уравнение прямой АВ, используя уравнение
прямой, проходящей через две точки:
,
.
АВ:
.
(
)
Вычислим величину
тангенса угла между прямыми АВ и ВС:
.
.
Ответ:
.