
- •III.Закрепление нового материала.
- •Тема № 4. Общее уравнения прямой. Виды уравнений прямой.
- •Тема № 5.Составление уравнения прямой.
- •2. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2.
- •3. Составить уравнение прямой, проходящей через точку а(-2, -3) и начало координат.
- •Тема № 6.Определение параллельности и перпендикулярности прямых.
- •Тема №7.Числовая последовательность и её предел.
- •Свойства бесконечно малых функций:
- •Бесконечно большие функции и их связь с бесконечно малыми.
- •Тема № 9.Раскрытие неопределенностей вида
- •Тема №10.Первый и второй замечательный пределы
- •Тема №11. Непрерывность функции.
- •1. Экономико-математические модели.
- •Общая задача линейного программирования
- •Основные теоремы линейного программирования.
- •Тема №16.Решение задач линейного программирования.
Теоретический материал для самостоятельного изучения .
Дисциплина: Элементы высшей математики
Тема №1. Системы n-линейных уравнений с m-переменными.
Теорема Кронекера-Капелли.
В общем виде система m линейных уравнений с n переменными записывается так:
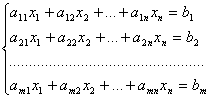 .
(1)
.
(1)
Числа
![]() называются коэффициентами
при переменных,
а
называются коэффициентами
при переменных,
а
![]() -
свободными
членами.
-
свободными
членами.
Совокупность
чисел
![]() называется решением
системы (1)
линейных уравнений, если при подстановке
их вместо переменных во все уравнения
они обращаются в верные равенства.
называется решением
системы (1)
линейных уравнений, если при подстановке
их вместо переменных во все уравнения
они обращаются в верные равенства.
Система mлинейных уравнений с n переменными называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.
Матрица ![]() ,
составленная из коэффициентов при
неизвестных, называется основной
матрицей системы
,
составленная из коэффициентов при
неизвестных, называется основной
матрицей системы ![]() :
:

Матрица

называется расширенной матрицей этой системы.
Элементарными преобразованиями системы линейных уравнений называют следующие операции:
1) сложение обеих частей одного уравнения с соответствующими частями другого, умноженных на одно и то же число, не равное нулю;
2) перестановка уравнений местами;
3) удаление из системы уравнений, являющихся тождествами.
Рассмотрим
матрицу А размера ![]() .
Выберем в этой матрице произвольно k
строк и k столбцов, где k ≤ m и k≤ n. Из
элементов, стоящих на пересечении
выделенных k строк и k столбцов, составим
определитель k-го порядка. Все такие
определители называют минорами k-го
порядка матрицы А.
.
Выберем в этой матрице произвольно k
строк и k столбцов, где k ≤ m и k≤ n. Из
элементов, стоящих на пересечении
выделенных k строк и k столбцов, составим
определитель k-го порядка. Все такие
определители называют минорами k-го
порядка матрицы А.
Рассмотрим систему m линейных уравнений с n неизвестными:
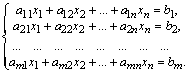
Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу, полученную из А добавлением столбца свободных членов, называют расширенной матрицей:
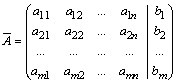 .
.
Ясно,
что ![]() ,
так как каждый минор матрицы А будет и
минором матрицы
,
так как каждый минор матрицы А будет и
минором матрицы ![]() ,
но не наоборот.
,
но не наоборот.
Теорема
Кронекера–Капелли (критерий совместности
системы линейных уравнений). Для
того чтобы система линейных уравнений
была совместной, необходимо и достаточно,
чтобы ранг матрицы системы был равен
рангу ее расширенной матрицы, т.е. ![]() .
.
Замечание. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг меньше числа неизвестных, то система имеет множество решений.
Пример. Исследовать систему линейных уравнений
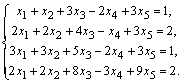
Решение. Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.

Далее умножим вторую строку на -2 и сложим с третьей, а затем сложим третью строку с последней. Имеем
 .
.
Ранг матрицы системы равен трем, так как матрица имеет три ненулевых строки, а ранг расширенной матрицы равен четырем. Тогда согласно теореме Кронекера-Капелли система не имеет решений.
Пример. Исследовать систему
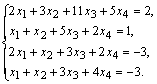
Решение. Выпишем
расширенную матрицу системы и поменяем
местами первую и вторую строки для того,
чтобы элемент ![]() равнялся
единице (так удобнее производить
преобразования матрицы).
равнялся
единице (так удобнее производить
преобразования матрицы).
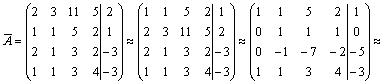
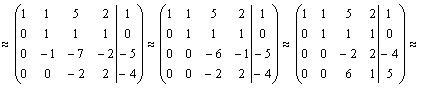
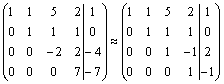 .
.
Имеем ![]() Ранги
матрицы системы и ее расширенной матрицы
совпали с числом неизвестных. Согласно
теореме Кронекера-Капелли система
уравнений совместна и решение ее
единственно.
Ранги
матрицы системы и ее расширенной матрицы
совпали с числом неизвестных. Согласно
теореме Кронекера-Капелли система
уравнений совместна и решение ее
единственно.
Тема №2. Векторы в пространстве. Скалярное произведение векторов в пространстве.
Величина,
характеризуемая числовым значением и
направлением, называется вектором.
Обозначения: ![]() или
или
![]() .
Геометрический вектор – это направленный
отрезок.
.
Геометрический вектор – это направленный
отрезок.
Для
вектора
–
точка ![]() –
начало, точка
–
начало, точка ![]() –
конец вектора. Координаты вектора:
–
конец вектора. Координаты вектора:
![]()
Модуль вектора
– это длина отрезка ![]() .
.
![]() .
.
Пусть
в пространстве задана тройка попарно
перпендикулярных единичных векторов
![]() ,
отложенных от некоторого начала – точки
О (рис.1).
,
отложенных от некоторого начала – точки
О (рис.1).
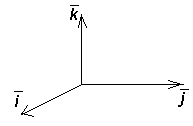
Рис.1.
Такую
тройку векторов называют прямоугольным
базисом в
пространстве. Совокупность начала О и
прямоугольного базиса
![]() называют прямоугольной системой
координат в пространстве.
называют прямоугольной системой
координат в пространстве.
Разложение
вектора
в базисе
имеет вид
![]() .
.
Скалярным
произведением
двух векторов
![]() и
и
![]() ,
обозначаемым
,
обозначаемым
![]() или
или
![]() ,
называется число, равное сумме произведений
соответствующих координат векторов,
т.е.
,
называется число, равное сумме произведений
соответствующих координат векторов,
т.е.
![]() .
.
Угол
между векторами
и
![]() вычисляется по формуле
вычисляется по формуле
![]() .
.
Свойства скалярного произведения:
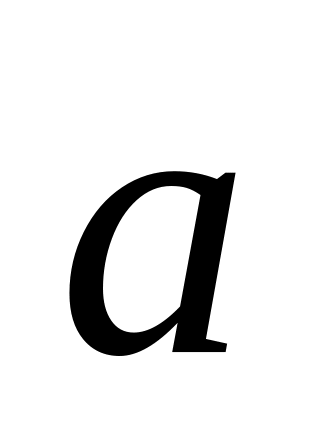
=
2;
=
2;
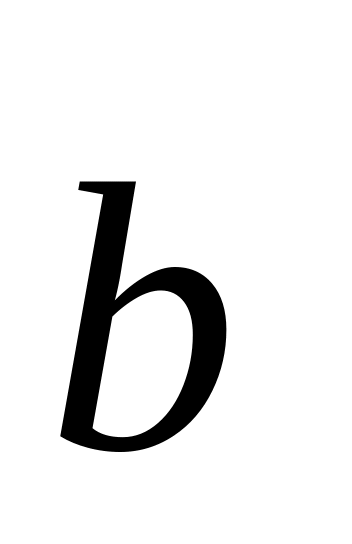 =
0, если
или
=
0 или
= 0.
=
0, если
или
=
0 или
= 0. = ;
( +
 )
=
+
;
)
=
+
;(m ) = (m ) = m( ); m=const
III.Закрепление нового материала.
Пример
1. Найти скалярное произведение векторов
![]() и
и
![]() .
.
Решение:
По формуле находим
![]()
Поскольку
![]() ,
то векторы перпендикулярны.
,
то векторы перпендикулярны.
Пример
2. Найти угол между векторами
![]() и
и
![]() .
.
Используем
формулу угла между векторами
![]() ,
,
![]()
![]() ,
получим
,
получим
![]()
Пример3.
Найти (5
+ 3
)(2
-
),
если
![]()
10
-
5
+
6
-
3
= 10![]() ,
,
т.к.
![]() .
.
Пример4.
Найти угол между векторами
и
,
если
![]()
![]() .
.
Т.е. = (1, 2, 3), = (6, 4, -2)
= 6 + 8 – 6 = 8:
![]() .
.
cos
=
![]()
Пример5.
Найти скалярное произведение (3
- 2
)(5
- 6
),
если
![]()
15
-
18
-
10
+
12
= 15![]()
+ 1236 = 240 – 336 + 432 = 672 – 336 = 336.
Пример6.
Найти угол между векторами
и
,
если
![]()
![]() .
.
Т.е. = (3, 4, 5), = (4, 5, -3)
= 12 + 20 - 15 =17 :
![]() .
.
cos
=
![]()
Пример7.
При каком m
векторы
![]() и
и
![]() перпендикулярны.
перпендикулярны.
= (m, 1, 0); = (3, -3, -4)
![]() .
.
Пример8.
Найти скалярное произведение векторов
![]() и
и
![]() ,
если
,
если
![]()
(
)(
)
=
![]()
![]()
![]() =
10 +
=
10 +
+ 27 + 51 + 135 + 72 + 252 = 547.
Тема № 3. Векторное, смешанное произведение векторов в пространстве.
Векторным
произведением векторов
и
называется вектор
![]() ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
1)
![]() ,
где
- угол между векторами
и
,
,
где
- угол между векторами
и
,
![]()
2) вектор ортогонален векторам и
3) , и образуют правую тройку векторов.
Обозначается:
![]() или
или![]() .
.

Свойства векторного произведения векторов:
1)
![]() ;
;
2)
![]() ,
если
или
=
0 или
=
0;
,
если
или
=
0 или
=
0;
3) (m ) = (m ) = m( );
4) ( + ) = + ;
5) Если заданы векторы (xa, ya, za) и (xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами , то
=
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .
Пример.
Найти векторное произведение векторов
![]() и
и
![]() .
.
= (2, 5, 1); = (1, 2, -3)
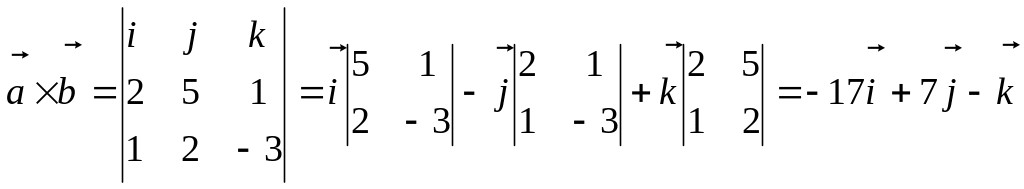 .
.
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3),С(0, 1, 0).
![]()
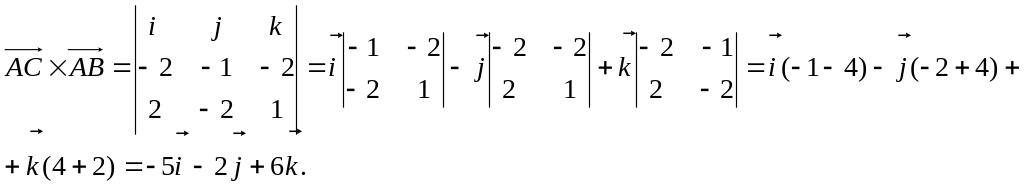
![]()
![]() (ед2).
(ед2).
Пример.
Доказать, что векторы
![]() ,
,
![]() и
и
![]() компланарны.
компланарны.
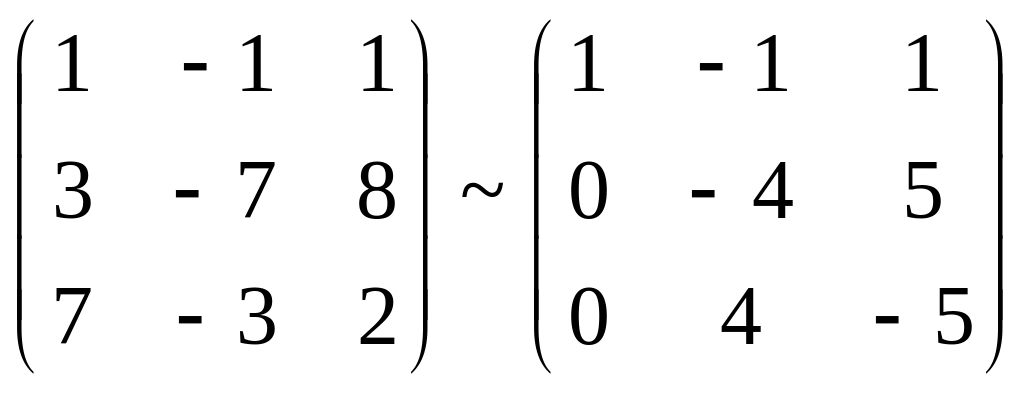 ,
т.к. векторы линейно зависимы, то они
компланарны.
,
т.к. векторы линейно зависимы, то они
компланарны.
Пример.
Найти площадь параллелограмма,
построенного на векторах
![]() ,
если
,
если
![]()
![]()
![]() (ед2).
(ед2).
Смешанным произведением векторов , и называется число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов и .
Обозначается
![]() или
(
,
,
).
или
(
,
,
).
Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах , и .
![]()
Свойства смешанного произведения:
1)Смешанное произведение равно нулю, если:
а) хоть один из векторов равен нулю;
б) два из векторов коллинеарны;
в) векторы компланарны.
2)![]()
3)![]()
4)![]()
5) Объем треугольной пирамиды, образованной векторами , и , равен
![]()
6)Если
![]() ,
,
![]() ,
то
,
то
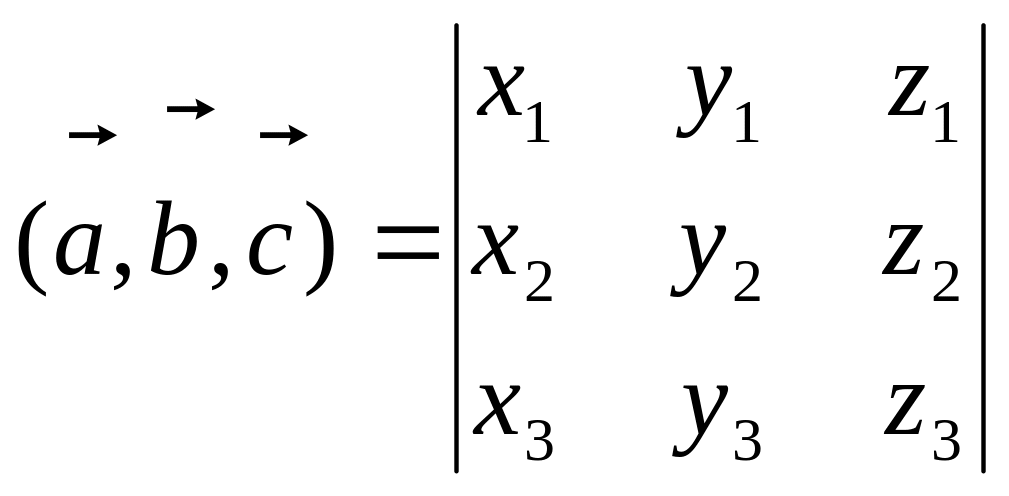
Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.
Найдем
координаты векторов:

Найдем смешанное произведение полученных векторов:
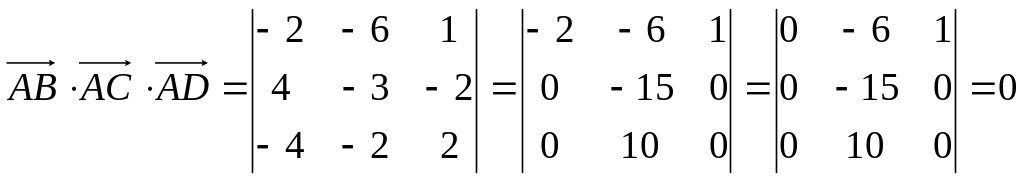 ,
,
Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.
