Mühazirə 16. Xətti funksionalin normasi

Tutaq ki, X normallaşmış fəzasında təyin olunmuş f(x) xətti kəsilməz funksional verilmişdir. Məlum teoremə əsasən f(x) funksionalı 0 nöqtəsində də kəsilməz olar və 0 nöqtəsinin ətrafında da məhduddur. Məlumdur ki, nöqtənin istənilən ətrafına mərkəzi bu nöqtədə olan elə kürə var ki, bu kürə tamamilə həmin ətrafa daxildir. Bu zaman f(x) xətti kəsilməz funksionalı mərkəzi 0 nöqtəsində müəyyən kürədə məhdud olar. F funksionalı xətti olduğundan bu funksional vahid kürədə ( ) məhduddur.

ədədinə f xətti kəsilməz funksionalın norması deyilir.

F xətti olduğundan nöqtəsi üçün

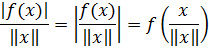
olar. Deməli, xətti kəsilməz funksionalın normasını

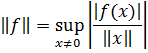
kimi təyin edə bilərik.

Bu axırıncı tərifdən aydındır ki, nöqtəsi üçün

olar. Buradan aydındır ki, xətti kəsilməz funksionalın normasını üçün

şərtini ödəyən c ədədləri çoxluğunun infimiumu kimi də təyin edə bilərik.

Mühazirə 17. Hilbert fəzasinda xətti kəsilməz funksionalin ümumi şəkli

Teorem : (Riss) H Hilbert fəzasında təyin olunmuş hər bir xətti kəsilməz f(x) funksionalı üçün elə elementi var ki, üçün f(x)=(x, ) olar. Bu zaman nöqtəsi yeganədir və tərsinə , f(x)=(x, ) kimi təyin olunan funksional xətti və kəsilməzdir.

İsbatı : kimi işarə edək. f xətti kəsilməz funksional olduğundan bu çoxluq boş deyil, çünki ən azından f(0)=0 olduğundan olar. Aydındır ki, elə 0-dan fərqli elementi var ki, yəni ( ) olar, yəni üçün (x, )=0 olar. Onda H fəzasının istənilən elementini x=y+ , y şəklində göstərmək olar. işarə edək. Onda aydındır ki, nöqtəsi üçün

(x, )=(y+ )=f( ( )+ f( )(y, )= f( )(y, ) və

f(x)=f(y+ )=f(y)+ f( )= f( olar. f funksionalı xətti olduğundan ( )=1 götürsək, görərik ki, f(x)=(x, ) olar. göstərək ki, bu cür seçilən nöqtəsi yeganədir. Doğrudan da, əgər f(x)=(x, ), f(x)=(x, ) olarsa, bu bərabərlikləri tərəf-tərəfə çıxsaq 0=(x, )- (x, )=(x, )

x nöqtəsi H fəzasından götürülmüş nöqtə olduğundan sonuncu bərabərlikdən

olduğunu alarıq. Bu zaman olar. f(x)=(x, ) kimi təyin olunan funksionalın xətti və kəsilməz olması aydındır.

Mühazirə 18. Xətti operator anlayişi.

OPERATORUN KƏSİLMƏZLİYİ VƏ MƏHDUDLUĞU.

Tutaq ki, X və Y topoloji fəzaları (hər bir nöqtənin ətrafı anlayışını daxil etmək mümkündür) verilmişdir və bu topoloji fəzalar xəttidir. Əgər X fəzasından Y fəzasına təsir edən f inikası aşağıdakı xassələri ödəyirsə, bu inikasa xətti operator deyilir:

1. üçün

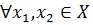2. və üçün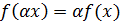

Tərif. Əgər nöqtəsinin ətrafı üçün nöqtəsinin ətrafı varsa ki, nöqtəsi üçün olsun, onda operatoru nöqtəsində kəsilməz adlanır.

Əgər operatoru fəzasının istənilən nöqtəsində kəsilməz olarsa, operatoru fəzasında kəsilməz adlanır.

Xüsusi halda, və fəzaları normallaşmış fəza olarsa, bu zaman operatorun kəsilməzliyinə aşağıdakı kimi tərif verilir:

Tərif. Tutaq ki, ədədinə görə ədədi var ki, şərtini ödəyən nöqtəsi üçün şərti ödənilir. Onda operatoruna nöqtəsində kəsilməz operator deyilir.

Tərif. Əgər operatoru məhdud çoxluğu məhdud çoxluğa inikas etdirərsə, bu zaman həmin operatora məhdud operator deyilir.

Teorem. Hər bir kəsilməz operator məhduddur.

Əgər operatoru xətti və kəsilməz olarsa, onda bu operatorun məhdudluğuna aşağıdakı kimi tərif verilir:

üçün .

MÜHAZİRƏ 19. XƏTTİ OPERATORUN NORMASI

Tutaq ki, normallaşmış fəzasından normallaşmış fəzasına təsir edən xətti operatoru verilmişdir. Əgər operatoru məhdud olarsa, onda tərifə əsasən ədədi var ki, üçün olar. Bu zaman bu şərti ödəyən c ədədlərinin ən kiçiyinə operatorunun norması deyilir və kimi işarə olunur.

Teorem. Tutaq ki, xətti operatoru məhduddur. Onda

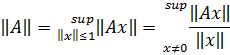
İsbatı: operatoru xətti və məhdud olduğundan məhdudluğun tərifinə əsasən üçün olar. Burada üçün olduğunu alarıq. Dəqiq yuxarı sərhədin tərifinə əsasən ədədi ifadəsini yuxarıdan məhdudlayan ədədlərin ən kiçiyinə deyilir, yəni c ədədlərinin ən kiçiyinə deyilir. Daha doğrusu,

olar. Digər tərəfdən, operatoru xətti olduğundan olar. Həmçinin, olduğundan bərabərliyin digər tərəfini alarıq.

MÜHAZİRƏ 20. OPERATORLARIN CƏMİ VƏ HASİLİ

Tutaq ki, xətti fəzasından xətti fəzasına təsir edən və operatorları verilmişdir. nöqtəsinə nöqtəsini uyğun qoyan operatora və operatorlarının cəmi deyilir və kimi işarə olunur.

Deməli, tərifə əsasən olar.

Tutaq ki, xətti fəzasından xətti fəzasına təsir edən operatoru verilmişdir. ədədinin operatoruna hasili kimi işarə olunur və

kimi təyin olunur.

Tutaq ki, və xətti fəzaları normallaşmış fəzalardır. Onda

operatorunun norması və operatorunun norması

olar.

Doğrudan da, elementi üçün

və deməli,

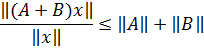
olduğundan axırıncı bərabərsizlikdə supremiuma keçsək, olduğunu alarıq. Həmçinin, nöqtəsi və ədədi üçün

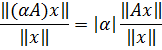
bərabərliyində supremiuma keçsək, olduğunu alarıq.

Tutaq ki, xətti fəzasından xətti fəzasına təsir edən operatoru və xətti fəzasından xətti fəzasına təsir edən xətti operatoru verilmişdir. nöqtəsinə nöqtəsini uyğun qoyan operatora operatoru ilə operatorunun hasili deyilir və kimi işarə olunur.

Göstərmək olar ki, nöqtəsi üçün

və deməli,

olar. Bu bərabərsizlikdə supremiuma keçsək, alınar.

Asanlıqla göstərmək olar ki, xətti operatorun ədədə hasili də xəttidir, xətti operatorların cəmi və hasili də xətti operatordur. Həmçinin, kəsilməz operatorun ədədə hasili, kəsilməz operatorların cəmi və hasili də kəsilməz operatordur.

Qeyd edək ki, xətti fəzasından xətti fəzasına təsir edən bütün mümkün xətti operatorlar çoxluğunu kimi işarə edirlər. Yuxarıda deyilənlərə əsasən bu fəza xətti fəzadır.