Mühazirə 14. Xətti funksionalin davami

XAN-BANAX TEOREMİ

Tutaq ki, L xətti fəzası, altfəzası, fəzasında təyin olunmuş b xətti funksionalı və L fəzasında təyin olunmuş f xətti funksionalı verilmişdir. Əgər funksionalı funksionalının fəzasından fəzasına davamı adlanır.

Teorem (Xan-Banax) Tutaq ki, xətti fəzası, altfəzası, fəzasında təyin olunmuş xətti funksionalı və fəzasında təyin olunmuş bircins qabarıq funksionalı verilmişdir. Əgər nöqtəsi üçün (bu zaman deyirlər ki, funksionalı funksionalına tabedir) olarsa, funksionalını fəzasına davam etdirmək olar və bu zaman nöqtəsi üçün funksionalının davamı olan funksionalı da şərtini ödəyir.

Isbatı : nöqtəsi götürək ki, olsun və elementi üçün şəklində olan nöqtələr çoxluğunu kimi işarə edək. Aydındır ki, olar. Əvvəlcə göstərək ki, funksionalını fəzasında fəzasına davam etdirmək olar.

funksionalını fəzasından fəzasına davamını ilə işarə edək, belə ki,

işarə etsək,

Onda (1) şərtinə əsasən

Əgər olarsa, (2) bərabərsizliyinə əsasən,

Əgər olarsa, (2) bərabərsizliyinə əsasən,

olduğundan

Onda (3) və (4) bərabərsizliyinə əsasən alırıq ki,

(5) şərtini ödəyən ədədi üçün aydındır ki,

funksionalı funksionalının fəzasından fəzasına davamı olar. Belə ki, funksionalının bircins qabarıq funksionalına tabelik şərti ödənilir.

elementi götürək və işarə edək. Isbat zamanı göstərdiyimiz qaydaya əsasən funksionalını fəzasından fəzasına davam etdirmək olar. Əgər hesabi sayda elementlər ilə fəzasının tamamlanması fəzasını verərsə, bu zaman prosesi bu qaydayla davam etdirməklə teoremi isbat etmiş olarıq.

Mühazirə 15.Xətti funksionalin kəsilməzliyi

Tutaq ki, L xətti fəzasında təyin olunmuş f(x) xətti funksionalı verilmişdir. Belə ki, L fəzasının hər bir nöqtəsinin ətrafı anlayışını daxil etmək mümkündür. (metrika daxil olunmuş fəzada hər bir nöqtənin ətrafı anlayışını daxil etmək olar)

Tərif : Tutaq ki, ədədinə görə nöqtəsinin ətrafı var ki, nöqtəsi üçün

şərti ödənilir. Onda f funksionalına nöqtəsində kəsilməz funksional deyilir.

Teorem 1: Əgər f xətti funksionalı L fəzasının hər hansı bir nöqtəsində kəsilməzdirsə, onda f funksionalı L fəzasının istənilən nöqtəsində kəsilməz olar.

İsbatı : Tutaq ki, f(x) funksionalı hər hansı nöqtəsində kəsilməzdir. Göstərək ki, f funksionalı nöqtəsində kəsilməzdir. nöqtəsinin

şərtini ödəyən ətrafını U ilə işarə edək. Onda aydındır ki,

çoxluğu nöqtəsinin ətrafı olar. nöqtəsi götürək. Aydındır ki,

olar. Digər tərəfdən f funksionalı xətti olduğundan

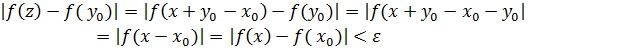
olar. Bu isə o deməkdir ki, f funksionalı nöqtəsində kəsilməzdir. Teorem

isbat olundu.

Teorem 2: f xətti funksionalının L fəzasında kəsilməz olması üçün zəruri və kafi şərt f funksionalının 0 nöqtəsinin müəyyən ətrafında məhdud olmasıdır.

İsbatı : (zərurilik) :Tutaq ki, f funksionalı L fəzasında kəsilməzdir. Onda f funksionalı xüsusi halda 0 nöqtəsində də kəsilməz olar. Bu isə tərifə əsasən o deməkdir ki, ədədinə görə 0 nöqtəsinin ətrafı var ki, olar (f(0)=0 olmasına əsasən). Bu isə o deməkdir ki, f(x) funksiyası məhduddur.

(Kafilik): Tutaq ki, 0 nöqtəsinin müəyyən U ətrafında f(x) funksionalı məhduddur. Onda tərifə əsasən ədədi var ki, üçün olar. ədədi götürək və V= işarə edək. Aydındır ki, V çoxluğu 0 nöqtəsinin müəyyən ətrafıdır və nöqtəsi üçün

olar. Bu isə o deməkdir ki, f funksionalı 0 nöqtəsində kəsilməzdir. Onda teorem 1-ə əsasən F funksionalı L fəzasının istənilən nöqtəsində kəsilməz

olar. Teorem isbat olundu.