Mühazirə 12. Xətti funksional anlayişi

Tutaq ki, L xətti fəzası verilmişdir. L fəzasında həqiqi ədədlər və ya kompleks ədədlər çoxluğuna təsir edən inikas funksional adlanır.

Tərif 1: Tutaq ki, L xətti fəzasında təyin olunmuş f funksionalı verilmişdir. Əgər olarsa, f funksionalına additiv funksional deyilir.

Tərif 2: Əgər nöqtəsi üçün olarsa, f funksionalına bircins funksional deyilir.

Tərif 3: Həm additiv, həm dəbircins olan funksionala xətti funksional deyilir.

Misal : fəzasından götürülmüş funksiyasına qarşı

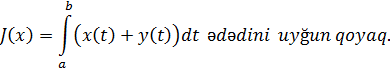
Aydındır ki, bu funksional xəttidir. Doğrudan da

Tərif 4: Əgər elementi üçün olarsa, f funksionalına qoşma bircins funksional deyilir.

Tərif 5: Additiv və qoşma-bircins olan funksionala qoşma-xətti və ya yarımxətti funksional deyilir.

Tutaq ki, L xətti fəzasında təyin olunmuş f xətti funksionalı verilmişdir. tənliyinin köklərinin əmələ gətirdiyi çoxluğa f funksionalının nüvəsi deyilir və Kerf kimi işarə olunur. Aydındır ki, və Kerf çoxluğu boş deyil, çünki, ən azı tənliyinin trivial həlli var. Əgər 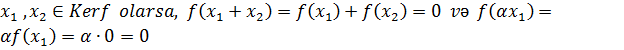olar. Bu isə o deməkdir ki, olar. Daha doğrusu Kerf çoxluğu L xətti fəzasının altfəzasıdır.

Mühazirə 13. Qabariq çoxluq və qabariq funksional anlayişi

Tutaq ki, L xətti fəzası verilmişdir və

şəklində olan bütün mümkün nöqtələr çoxluğuna nöqtələrini birləşdirən parça deyilir.

Tutaq ki, çoxluğu verilmişdir və çoxluğunun istənilən 2 nöqtəsini birləşdirən parça da çoxluğuna daxil olarsa, bu zaman həmin çoxluğa qabarıq çoxluq deyilir.

Əgər nöqtələrini birləşdirən parçadan bu nöqtələri atdıqdan sonra alınan çoxluğa nöqtələrini birləşdirən açıq parça deyilir.

Tərif 1: Tutaq ki, xətti fəzası və çoxluğu verilmişdir və ədədi var ki, şərtini ödəyən elementi üçün . Bütün bu cür nöqtələri çoxluğuna çoxluğunun nüvəsi deyilir.

Tərif 2: Nüvəsi boş olmayan qabarıq çoxluğa qabarıq cisim deyilir.

Tərif 3: Tutaq ki, xətti fəzası və bu fəzada təyin olunmuş funksionalı verilmişdir. Əgər elementləri və ədədi üçün olarsa, funksionalına qabarıq funksional deyilir.

Tərif 4: Tutaq ki, elementi və ədədi üçün şərti ödənilir. Onda p funksionalına müsbət bircins funksional deyilir.

Tərif 5: Qabarıq və müsbət bircins olan funksionala bircins qabarıq funksional deyilir.

Tutaq ki, L xətti fəzasında təyin olunmuş p bircins qabarıq funksionalı verilmişdir. Onda elementləri üçün

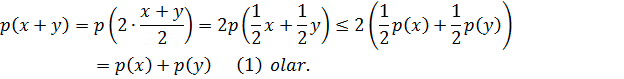
Indi isə, bircins qabarıq funksionalının bəzi əsas xassələrini qeyd edək:

Xassə 1: Tutaq ki, xətti fəzasında təyin olunmuş bircins qabarıq funksionalı verilmişdir. Onda olar.

Isbatı : funksionalı bircins qabarıq olduğundan müsbət bircinsdir. Onda Bu bərabərlikdə götürsək, ədədi üçün olduğunu alarıq, yəni,

Xassə 2: Tutaq ki, L xətti fəzasında təyin olunmuş bircins qabarıq funksionalı verilmişdir. Onda elementi üçün olar.

Isbatı : elementi götürək. Onda (1) bərabərsizliyinə və xassə 1-ə əsasən

Xassə 3: Tutaq ki, L xətti fəzası və bu fəzada təyin olunmuş bircins qabarıq funksionalı verilmişdir. Onda elementi və ədədi üçün olar.

Isbatı : Aydındır ki, xassə 1-ə əsasən olduqda bu bərabərsizlik doğrudur, funksionalı müsbət bircins olduğuna əsasən isə, olduqda olar və deməli, olduqda bu bərabərsizlik doğrudur. Tutaq ki, . Onda xassə 1-ə və (1) bərabərsizliyinə əsasən 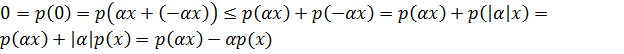olar. Buradan isə, olduqda

olduğunu alarıq. Nəticədə aldıq ki, ədədi üçün olar. Xassə isbat olundu.

Tutaq ki, L xətti fəzası və qabarıq cismi verilmişdir. elementinə qarşı

ədədini uyğun qoyan funksionala Minkovski funksionalı deyilir. Göstərmək olar ki, üçün olar və Minkovski funksionalı bircins qabarıq funksionaldır.