Mühazirə 10. Tam evklid fəzasi. Riss-fişer teoremi

Tutaq ki, L Evklid fəzası verilmişdir. Əgər bu fəza

metrikasına nəzərən tam fəza olarsa, L fəzasına tam Evklid fəzası deyilir.

Tutaq ki, L tam Seperabel-Evklid fəzası və bu fəzadan götürülmüş ortonormal sistemi verilmişdir. Aydındır ki, elementi üçün bu elementin Furye sırasına yığılan olması üçün zəruri və kafi şərt Bessel bərabərsizliyinə əsasən elementinin Furye əmsallarından düzəldilmiş

sırasının yığılan olmasıdır. Aşağıdakı teorem onu göstərir ki, bu şərt həm də kafidir.

Teorem 1:(Riss-Fişer) Tutaq ki, L tam Evklid fəzası və bu fəzadan götürülmüş ortonormal sistemi verilmişdir. Onda

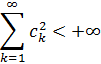
şərtini ödəyən ədədləri üçün elementi var ki,

Isbatı :

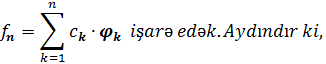
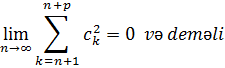
Bu isə o deməkdir ki, ardıcıllığı fundamentaldır. L fəzası tam olduğundan hər bir fundamental ardıcıllıq yığılandır və deməli, ardıcıllığı yığılandır.

Aydındır ki, olduqda və Koşi-Bunyakovski bərabərsizliyinə əsasən,

olduqda (2) bərabərliyində limitə keçsək,

alarıq.

Bu bərabərlikdə olduqda limitə keçsək,

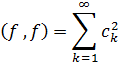
Teorem isbat olundu.

Isbatsız olaraq aşağıdakı teoremi qeyd edək

Teorem 2: Tutaq ki , L tam Seperabel Evklid fəzası və bu fəzadan götürülmüş ortonormal sistemi verilmişdir. sisteminin qapalı olması üçün zəruri və kafi şərt bu sistemin hər bir elementinə ortoqonal olan L fəzasından götürülmüş sıfır elementin olmamasıdır.

Mühazirə 11. Hilbert fəzasi. Hilbert fəzasinin izomorfluğu

Tərif 1: Tam sonsuz ölçülü Evklid fəzası Hilbert fəzasıdır.

Biz bu mövzuda adətən Seperabel- Hilbert fəzasından danışacağıq:

Tərif 2: Tutaq ki, L və L^* Evklid fəzaları arasında qarşılıqlı birqiymətli uyğunluq var və

1. 

2. 

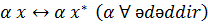
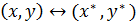3. şərti ödənir. Onda L və 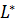fəzaları bir-birinə izomorf olan fəzalar adlanır.

Aydındır ki, sonlu ölçülü Evklid fəzaları çoxluğunda eyniölçülü olan Evklid fəzaları bir-birinə izomorfdur. Deməli, ölçülü Evklid fəzası fəzasına izomorfdur. Lakin sonsuz ölçülü Evklid fəzalarında bu fakt doğru olmaya da bilər. Məsələn, Evklid fəzaları sonsuz ölçülüdür, lakin izomorf deyillər. Çünki ən azı tam Evklid fəzasıdır, lakin, Evklid fəzası tam deyil.

Misal : fəzası Seperabel- Hilbert fəzasıdır.

Teorem : İstənilən iki Seperabel-Hilbert fəzaları bir-birinə izomorfdur.

Isbatı : Əvvəlcə göstərək ki, Seperabel-Hilbert fəzası fəzasına izomorfdur. fəzasında hər hansı ortonormal sistemi götürək. Aydındır ki, fəzasından götürülmüş elementinə qarşı bu elementin Furye əmsallarını uyğun qoymaq olar. Bessel bərabərsizliyinə əsasən,

elementi götürək. Bu zaman

Onda Riss-Fişer teoreminə əsasən, elementi var ki, ədədləri f elementinin Furye əmsalları olar. Bu qaydayla biz fəzaları arasında qarşılıqlı birqiymətli uyğunluq yaratmış olarıq:

Tutaq ki,

Burada elementinin, elementinin Furye əmsallarıdır. Onda asanlıqla göstərmək olar ki,

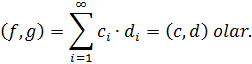
Deməli, istənilən Seperabel-Hilbert fəzası fəzasına izomorfdur. Buradan isə alarıq ki, istənilən iki Seperabel-Hilbert fəzası bir-birinə izomorfdur. Teorem isbat olundu.