Mühazirə 6. Normallaşmiş fəza

Tutaq ki, L xətti fəzası verilmişdir və L fəzasında həqiqi ədədlər çoxluğuna təsir edən funksiyası(funksionalı) aşağıdakı şərtləri ödəyir:

1) üçün

2)

3) Onda p funksionalı L fəzasında norma adlanır. Norma daxil edilmiş fəzaya normallaşmış fəza deyilir. Hər bir elementinin norması kimi işarə olunur.

Hər bir normallaşmış fəza metrik fəzadır. Doğrudan da, bunu göstərmək üçün metrikanı kimi daxil etmək kifayətdir.

Misal : ölçülü Evklid fəzasında hər bir nöqtələrinin normasını

kimi daxil etmək olar. Aydındır ki, bu cür daxil olunmuş norma normanın əsas xassələrini ödəyir.

Məlumdur ki, xətti fəzanın altfəzası dedikdə toplama və ədədə vurma əməlinə görə qapalı olan altçoxluq başa düşülür.

Tutaq ki, L normallaşmış fəzası verilmişdir. Əgər çoxluğu L xətti fəzasının altfəzası və L₀ altfəzası qapalı çoxluq olarsa, L₀ çoxluğuna L normallaşmış fəzasının altfəzası deyilir.

Qeyd edək ki, hər bir sonlu ölçülü normallaşmış fəzada xətti fəzanın istənilən altfəzası qapalı çoxluq olur. Lakin sonsuz ölçülü fəzada bu doğru olmaya da bilər. Məs: fəzasında normanı

kimi daxil edək və parçasında təyin olunmuş bütün çoxhədlilər çoxluğunu ilə işarə edək. Aydındır ki, xəti fəzasının altfəzasıdır. Lakin normallaşmış fəza kimi -in altfəzası deyil, çünki, -in qapanması -dən daha geniş olan çoxluğuna bərabərdir, yəni, qapalı çoxluq deyil.

Tam normallaşmış fəzaya Banax fəzası və ya B fəzası deyilir.

Mühazirə 7. Evklid fəzasi

Tutaq ki, L xətti fəzası verilmişdir və elementləri cütünə kimi işarə olunan yeganə həqiqi ədəd qarşı qoyan funksional aşağıdakı xassələri ödəyir:

1. 

2. 

3. 

4. 

Onda deyirlər ki, L fəzasında skalyar hasil təyin olunmuşdur.

Skalyar hasil təyin olunan xətti fəzaya Evklid fəzası deyilir. Daha doğrusu Evklid fəzası dedikdə xətti fəza və bu fəzada təyin olunmuş skalyar hasil başa düşülür.

ədədi və elementləri götürək. Aydındır ki, skalyar hasilin məlum olan xassələrinə əsasən

Əgər elementləri xətti asılı deyilsə olar. Digər tərəfdən a nəzərən kvadratik üçhədli olduğundan məlumdur ki, şərtindən alırıq ki, həqiqi kökləri yoxdur və deməli, diskriminant mənfidir:

Asanlıqla yoxlamaq olar ki, hər bir Evklid fəzası normallaşmış fəzadır, bunun üçün

Normanın bu cür daxil olunmasını (1) bərabərsizliyində nəzərə alsaq, xətti asılı olmayan elementlər üçün

olduğunu alarıq.

Aydındır ki, x və y elementləri xətti asılı olarsa, (2) bərabərsizliyi bərabərliyə çevrilər. Onda elementləri üçün

olduğunu alarıq.

(3) bərabərsizliyi Koşi-Bunyakovski bərabərsizliyi adlanır. Əgər olarsa, x və y elementlərinə ortoqonal elementlər deyilir.

MÜHAZİRƏ 8. ORTOQONAL VƏ ORTONORMAL SİSTEMLƏR.BAZİS ANLAYIŞI.

Tutaq ki, L Evklid fəzası və bu fəzadan götürülmüş elementlər sistemi verilmişdir. Əgər olduqda =0 olarsa, sistemi ortoqonal sistem adlanır. Əgər

olarsa, sistemi ortonormal sistem adlanır.

Göstərmək olar ki, ortoqonal sistem xətti asılı deyil. Doğrudan da əgər

olarsa, bu ayrılışın hər tərəfinin skalyar hasilinə baxsaq

olduğunu alarıq.

Tutaq ki, L Evklid fəzasında ortoqonal sistemi verilmişdir. Əgər sisteminin elementlərinin xətti kombinasiyaları çoxluğunun qapanması bütün L fəzasını verərsə, yəni sistemi L fəzasında sıx olarsa, bu sistemə L fəzasında ortoqonal bazis deyilir. Əgər bu zaman sistemi ortonormal olarsa, bu sistem ortonormal bazis adlanır.

Misal : Rⁿ fəzasında

--------------------

ortonormal sistemi bazis təşkil edir. Doğrudan da fəzasının hər bir x elementini şəklində göstərmək mümkündür.

Əgər L Evklid fəzasında hesabi sıx çoxluq varsa, bu fəza Seperabel-Evklid fəzası adlanır. Məsələn, l₂ fəzasında

-----------------------

sistemi ortonormal bazis təşkil edir və bu bazisin elementləri hesabi sayda olduğundan l₂ fəzası Seperabel-Evklid fəzasıdır.

Teorem : Tutaq ki, L Evklid fəzasında xətti asılı olmayan elementlər sistemi verilmişdir. Onda L fəzasında elə ortonormal sistemi var ki,

1).

2). olar.

Isbatı : Verilmiş sisteminə uyğun olaraq sistemini induktiv olaraq aşağıdakı qaydada quraq:

götürək. Belə ki,

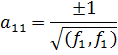
Tutaq ki, natural ədədləri üçün -ları təyin etmişik. Induktiv olaraq təyin edək. Onda

Aydındır ki,

kimi təyin edək. Göründüyü kimi, bu qayda ilə qurulan sistem ortonormaldır və qeyd olunan xassələri ödəyir. Teorem isbat olundu.

MÜHAZİRƏ 9. EVKLİD FƏZASINDA FURYE SIRASI

Tutaq ki, L Evklid fəzası və bu fəzada ortonormal sistemi verilmişdir. elementi götürək və

sırasını düzəldək, burada

1. sırasına f elementinin Furye sırasına ayrılışı, ədədlərinə

isə, f elementinin Furye sırasının əmsalları deyilir.

Indi isə, (1) sırasının yığılan olub-olmamasını, yığılandırsa, bu sıranın cəminin f elementinə bərabər olub-olmamasını araşdıraq.

ədədlərini elə seçək ki,

sırası ilə f elementi arasındakı məsafə minimal olsun.

işarə edək. Aydındır ki,

(3) olar.

Göründüyü kimi ifadəsi minimal qiymətini olduqda alır. Deməli, (2) şəklində olan sıralardan məsafəcə f elementinə ən yaxın olan sıra f elementinin Furye sırasıdır. Bu zaman

olduğunu alarıq. (5) bərabərsizliyi istənilən n natural ədədi üçün doğru olduğundan və bu bərabərsizliyin sağ tərəfi n-dən asılı olmadığına görə

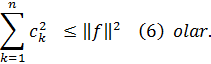
(6) bərabərsizliyi Bessel bərabərsizliyi adlanır. Bu bərabərsizlikdən aydındır ki, Furye əmsallarının kvadratından düzəldilmiş sıra yığılandır.

Tərif : Tutaq ki, L Evklid fəzasında ortonormal sistemi verilmişdir. Əgər elementi üçün

(7) ortonormal sistemi L Evklid fəzasında qapalı sistem adlanır, burada

(8) bərabərliyi Parseval bərabərliyi adlanır.

(4) bərabərliyindən aydındır ki, əgər (7) sistemi qapalı olarsa, yəni Parseval bərabərliyi ödənərsə,

olar. Bu isə o deməkdir ki, bu zaman, yəni Parseval bərabərliyi ödəndikdə f elementinin Furye sırası bu elementin özünə yığılır.

Teorem : Seperabel-Evklid fəzasında ortonormal sistemin qapalı olması üçün zəruri və kafi şərt bu sistemin tam(dolu) olmasıdır.

Isbatı : (zərurilik) Tutaq ki, sistemi L Seperabel-Evklid fəzasında qapalıdır. Onda aydındır ki, bu zaman elementinin Furye sırası f elementinin özünə yığılır. Daha doğrusu, f elementinə (7) sisteminin elementlərinin xətti kombinasiyaları ilə yaxınlaşmaq mümkündür. Bu isə o deməkdir ki, (7) sistemi dolu sistem təşkil edir.

(kafilik): Tutaq ki, (7) sistemi dolu sistemdir. Onda tərifə əsasən (7) sisteminin elementlərinin xətti kombinasiyaları vasitəsilə f elementinə yaxınlaşmaq mümkündür(yəni, aproksimasiya etmək). (7) sisteminin elementlərinin xətti kombinasiyalarından f -ə ən yaxşı aproksimasiya olunan f elementinin Furye sırasıdır. Deməli, bu zaman f elementinin Furye sırası bu elementin özünə yığılır. Bu isə o deməkdir ki, Parseval bərabərliyi ödənir və deməli, (7) sistemi qapalıdır. Teorem isbat olundu.

Biz bu mövzuda elementin ortonormal sistem üzrə Furye sırasına ayrılışını göstərdik. Indi isə elementin ortoqonal sistem üzrə Furye sırasına ayrılışını yazaq:

Tutaq ki, L Evklid fəzası və bu fəzada ortoqonal sistemi verilmişdir.

Aydındır ki, olduqda

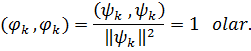
Deməli, bu qaydayla qurulan sistemi ortonormal sistem olar.

elementi götürək və işarə edək. Onda məlumdur ki, f elementinin Furye sırasına ayrılışı

(9) sırası f elementinin ortoqonal sistem üzrə Furye sırasına ayrılışı adlanır.