Mühazirə 29. Sixilmiş inikas prinsipinin fredholm inteqral tənliklərə tətbiqi
Aşağıdakı kimi Fredholm tip inteqral tənliyə baxaq:
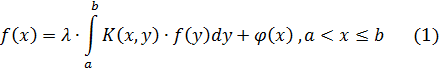
Burada
parametrdir,
parçasında kəsilməz olan verilmiş funksiyadır, verilmiş 
nüvəsi isə 
düzbucaqlısında kəsilməz olduğundan məhduddur, yəni,
ədədi var ki, 
nöqtəsi üçün 
olar.
Aydındır
ki,
Bu
isə o deməkdir ki, 
olduğundan
inikası sıxılmış inikasdır. Onda sıxılmış inikas
prinsipinə əsasən
şərti
daxilində 
tənliyinin, yəni (1) inteqral tənliyinin yeganə həlli var.
Qeyd
edək ki, (1) inteqral tənliyi üçün ardıcıl yaxınlaşmalar
aşağıdakı kimi qurulur:
Burada
funksiyası istənilən qaydada seçilmiş kəsilməz funksiyadır.
Aydındır ki, bu zaman 
funksiyalar ardıcıllığının limiti (1) tənliyinin həlli
olur.
MÜHAZİRƏ 30. SIXILMIŞ İNİKAS PRİNSİPİNİN VOLTER TİP İNTEQRAL TƏNLİKLƏRƏ TƏTBİQİ
Teorem
:
Tutaq ki, X
tam metrik fəzasından özünə təsir edən 
inikası kəsilməzdir və
natural ədədi var ki, 
inikası sıxılmış inikasdır. Onda
inikasının yeganə tərpənməz nöqtəsi var, yəni 
tənliyinin yeganə həlli var.
Indi isə bu teoremdən istifadə edərək tip inteqral tənliyə sıxılmış inikas prinsipini tətbiq edək:
Tutaq ki,
inteqral
tənliyi verilmişdir, burada
parçasında kəsilməz olan verilmiş funksiyadır, 
düzbucaqlısında verilmiş kəsilməz funksiyadır,
parametrdir,
f
isə axtarılan funksiyadır. (1) inteqral tənliyi Volter
tip inteqral tənlik
adlanır.
Aydındır
ki, 
kəsilməz funksiyaları üçün
-----------------------------------------------------
olduğundan
burada
Riyazi analiz kursundan məlumdur ki,
Onda
natural ədədi var ki,
olar.
Bu isə (2) bərabərliyinə əsasən o deməkdir ki, 
sıxılmış
inikasdır. Onda qeyd etdiyimiz teoremə əsasən
inikasının yeganə tərpənməz nöqtəsi var, yəni,
və ya (1) tənliyinin yeganə həlli var.
Qeyd edək ki, Fredholm tip inteqral tənliklərə sıxılmış inikas prinsipini tətbiq etmək üçün
şərti
qoyulmuşdur, lakin, Volter tip inteqral tənliyə sıxılmış
inikas prinsipini tətbiq etmək üçün 
parametri üzərinə heç bir əlavə şərt qoyulmur.