Funksional analiz

Mühazirə 1. Xətti fəza anlayişi. Xətti fəzanin ölçüsü

Tutaq ki,boş olmayan L çoxluğu aşağıdakı xassələri ödəyir:

1. elementlərinə qarşı bu elementlərin cəmi adlanan və x+y kimi işarə olunan 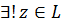elementi var ki, z=x+y

1. üçün x+y=y+z

2. üçün x+(y+t)=(x+y)+t

3. Sıfır adlanan və “0” kimi işarə olunan elementi var ki, üçün x+0=x

4. elementi üçün bu elementin əksi adlanan və (-x) kimi işarə olunan elementi var ki, x+y=0 olar, burada y= -x

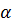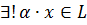2. elementi və ədədi(həqiqi və ya kompleks) üçün ədədinin x elementinə hasili adlanan və kimi işarə olunan elementi var ki,

1. 

2. 

3. 

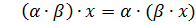
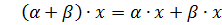
4. olar. Onda L çoxluğuna xətti fəza deyilir. Deməli, xətti fəza dedikdə toplama və ədədə vurma əməlinə görə qapalı olan çoxluq başa düşülür. Daha doğrusu, çoxluğun 2 elementinin cəmi də bu çoxluğa daxildirsə və çoxluğun elementinin ədədə hasili də bu çoxluğa daxildirsə, bu çoxluq xətti fəza adlanır.

Tutaq ki, L və xətti fəzaları arasında qarşılıqlı birqiymətli uyğunluq yaratmaq mümkündür, belə ki, olduqda x+ y və ədədi üçün . Onda L və xətti fəzaları izomorf xətti fəzalar adlanır.

Tutaq ki, L xətti fəzası verilmişdir. Əgər elementləri üçün heç olmazsa biri sıfırdan fərqli olan ədədləri varsa ki, olsun. Onda elementləri xətti asılı adlanır. Əks halda ,yəni, bərabərliyi yalnız və yalnız olduqda doğru olarsa, elementlərinə xətti asılı olmayan elementlər deyilir.

Əgər L xətti fəzasının sayda xətti asılı olmayan elementləri varsa və (n+1) sayda elementləri xətti asılı olarsa, bu zaman n natural ədədi L fəzasının ölçüsü adlanır.

Tutaq ki, L xətti fəzası verilmişdir və . Əgər və ədədi üçün x+y və olarsa, çoxluğu L çoxluğunun alt fəzası adlanır.

n ölçülü xətti fəzanın xətti asılı olmayan n sayda elementlər sistemi bu xətti fəzanın bazisi adlanır.

Mühazirə 2. Metrik fəza. Izometriya

Tutaq ki, X çoxluğu verilmişdir. Əgər elementlərinə qarşı yeganə həqiqi ədədi qarşı qoyan inikas aşağıdakı xassələri ödəyirsə, inikasına metrika deyilir:

1. 

2. 

3. 

Bu zaman deyirlər ki, X çoxluğunda metrika təyin olunmuşdur.

Tutaq ki, X çoxluğunda metrikası verilmişdir. Bu zaman (x, ) cütü metrik fəza adlanır.

Misal 1: Tutaq ki, hər hansı X çoxluğu verilmişdir. Bu çoxluqda həmişə aşağıdakı kimi metrika təyin etmək mümkündür.

Misal 2: həqiqi ədədlər çoxluğunu götürək

kimi metrika daxil olunur

Misal 3: parçasında təyin olunmuş kəsilməz funksiyalar çoxluğunda yəni, çoxluğunda metrikanı

kimi daxil etmək olar. Doğrudan da

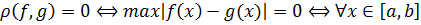1. üçün f(x)=g(x)

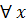2. üçün olduğundan olar.

3. funksiyaları üçün olduğundan bu bərabərsizliyin hər iki tərəfindən maksimuma keçsək, 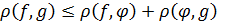alarıq.

Bəzi fəzaların metrik fəza olmasını göstərmək üçün aşağıdakı bərabərsizliklərdən geniş istifadə olunur:

Minkovski bərabərsizliyi

Hölder bərabərsizliyi

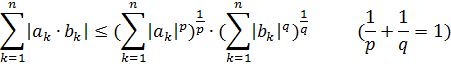
Bir çox hallarda qısa olaraq metrik fəzasının əvəzinə X kimi də yazırlar. Daha doğrusu, X metrik fəzası verilmişdir dedikdə X çoxluğu və bu çoxluqda verilmiş metrika başa düşülür. Tutaq ki, metrik fəzası verilmişdir. Aydındır ki, X çoxluğunun altçoxluğunda da metrikanı kimi daxil etmək olar. Onda metrik fəzasına metrik fəzasının altfəzası deyilir.

Tutaq ki, metrik fəzaları və inikası verilmişdir.

Tərif :Tutaq ki, ədədinə görə var ki, şərtini ödəyən elementi üçün şərti ödənilir. Onda f inikası nöqtəsində kəsilməz adlanır.

Tutaq ki, metrik fəzaları və inikası verilmişdir. Əgər f inikası qarşılıqlı birqiymətli və f , inikasları X çoxluğunda kəsilməz olarsa, f inikası homoemorf inikas, X və Y metrik fəzaları isə homoemorf fəzalar adlanır.

Tutaq ki, metrik fəzaları verilmişdir və və inikası biyektivdir. Əgər üçün olarsa, metrik fəzaları izometrik metrik fəzalar adlanır.