Пара   играет роль закрытого ключа RSA и держится в секрете.

Разработка алгоритма решения задачи

Решение поставленной задачи следует разбить на несколько подзадач:

1. Генерация открытого и закрытого ключей.

2. Шифрование текста.

3. Разработка пользовательского интерфейса.

Алгоритм генерации ключей содержит следующие шаги:

1. Выбор двух простых чисел p и q.

2. Вычисление произведения этих чисел(модуля) - n.

3. Вычисление функции Эйлера.

4. Выбор открытой экспоненты - e.

5. Вычисление секретной экспоненты - d.

Шифрование текста:

1. Открытие тесктового файла/ввод текста в поле.

2. Шифрование каждого символа исходя из его номера в таблице ASCII.

3. Замена текста зашифрованным сообщением.

Разработка программы

Для генерации простых чисел создадим функцию getSimpleRandomNumber(). Основной выглядит так:

repeat

random_number := random(5000);

until isSimpleNumber(random_number);

Как видно из кода, с помощью системной функции random генерируется случайное число от 0 до 5000, а затем оно проверяется на простоту с помощью функции isSimpleNumber(). Так как проверка на простоту числа достаточно сложна, числа, по итогу, являются псевдопростыми. Для проверки на простоту используется следующий алгоритм:

1. Проверка на существование остатка от деления на набор простых чисел от 2 до 251 – это позволит увеличить вероятность того, что это простое число примерно до 80%. Если остаток равен 0, то число не является простым.

2. Выполняется тест Миллера-Рабина с количеством раундов равному количеству бит в числе. Это вероятностный полиномиальный тест простоты. Он позволяет эффективно определить, является ли данное число составным. Однако, с его помощью нельзя строго доказать простоту числа, поэтому он вероятностный.

После того, как найдены простые числа и вычислено их произведение, находится функция Эйлера.

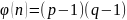
Выбор открытой экспоненты происходит следующим образом:

1. Выбирается начальное значение для открытой экспоненты(можно выбрать 3, но для криптостойкости было выбрано число 65537)

2. Далее происходит вычисление наибольшего общего делителя.

3. Если он не равен 1, увеличиваем на 2 значение открытой экспоненты и переходим на предыдущий пункт.

Секретная экспонента вычисляется по формуле:

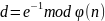
Эта функция называется модинверс. Так как во время вычислении этой функции используются достаточно большие числа, которые не входят в диапазон стандартных типов, было решено использовать внешний модуль Numerics для работы с большими числами. Он предоставляет класс BigInteger и основные операции для работы с этим типом. Так же в нём присутствует и операция вычисления обратного модуля. Ниже представлена моя собственная реализация для стандартных типов:

function modinv(a, m: longint): longint;

var

i, j, y, x: extended;

b, c: longint;

begin

b := m;

c := a;

i := 0;

j := 1;

while c <> 0 do

begin

x := b / c;

y := b mod c;

b := c;

c := round(y);

y := j;

j := i - j * x;

i := y;

end;

if i < 0 then

i := i + m;

modinv := round(i);

end;

После этого генерация ключей закончена. Ключи представляют собой связку из двух значений {e, n} и {d, n}.

Шифрование выполняется по формуле:

M – сообщение, с – зашифрованное сообщение.

В роли сообщения m было решено использовать номер символа из таблицы ASCII. Таким образом, в текстовом сообщении шифруется каждый символ отдельно. Шифрование строки происходит с помощью функции encryptString(string), внутри который каждый байт шифруется с помощью функции encryptByte(integer). Вычисление зашифрованного байта происходит с помощью функции ModPow из модуля Numerics. На выходе получается строка каждый зашифрованный байт которой разделён пробелом.

Расшифровка сообщения осуществляется по формуле:

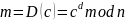
Вычисление исходного сообщение происходит с помощью функций decryptString и decryptByte. Так же используется функция ModPow. В них происходит разделение полученной строки на слова и вычисление каждого отдельного байта.

Для удобства пользователя было решено создать оконный интерфейс:

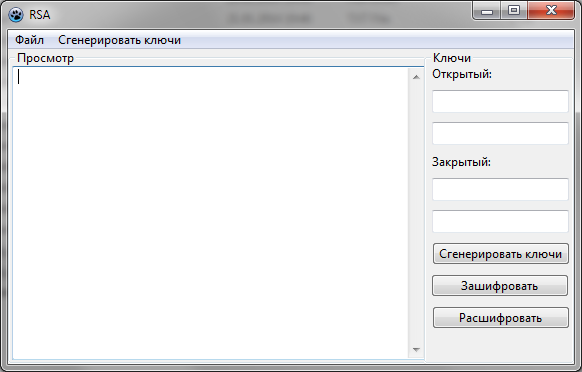
В меню присутствуют команды для открытия, сохранения файла, генерации ключей и выход из программы. При команде открытии файла открывается диалог выбора, а его содержимое отображается в большом поле. При нажатии на кнопку «Зашифровать» проверяется содержимое полей открытого ключа, если они не пусты, производится шифрование и его результат заменяет содержимое текстового поля. Зашифрованный текст можно сохранить с помощью команды меню «Сохранить». При вызове команды откроется диалог выбора расположения и имени файла, после выбора файл будет сохранён. По нажатию на кнопку «Расшифровать» происходит проверка полей закрытого ключа, необходимых для расшифровки и расшифровывается текст из главного текстового поля. После расшифровки текст отображается в нём же. По нажатию на кнопки генерации ключей происходит их генерация и занесение данных в поля ключей.

Тестирование программы.

Данная программа может зашифровать любой .txt файл, а так же вы можете набрать текст в окне программы и он будет зашифрован.

Заключение

В ходе работы над курсовой работой был изучен и реализован алгоритм RSA. Приложение реализовано для ОС Windows, служит для шифрования текстовых файлов. С его помощью можно как зашифровать сообщение, так и, имея закрытый ключ, расшифровать.

Приложение имеет понятный и простой пользовательский интерфейс. Так же присутствует меню. Оно может использоваться для завершения программы, выбора текстового файла, сохранения и генерации ключей

Список литературы

1. Интернет ресурсы – www.wikipedia.org, groups.google.com, www.xakep.ru, ref.rushkolnik.ru, www.wikisec.ru

15