Классификация и применение операционных усилителей
В результате поисков и эволюции схемотехнических и технологических решений был создан ряд ОУ, которые согласно квалификации по ГОСТ 4.465 - 86 делятся на:
универсальные (общего применения), у которых Кu = 103 - 105; f1 = 1,5 - 10 МГц;
прецизионные (инструментальные), у которых Кu > 0.5*106 и гарантированные малые уровни Uсм < 0,5мВ и его дрейфа;
быстродействующие со скоростью нарастания выходного напряжения νUвых > 20 В/мкс;
регулируемые (микромощные) с током потребления Iпот < 1мА;
мощные и высоковольтные ОУ;
многоканальные.
На основе операционных усилителей (ОУ) создаются схемы, предназначенные для выполнения математических операций над входными сигналами (сложение, вычитание, интегрирование, выделение модуля функции, выпрямление и т.п.). Такие схемы находят широкое применение в устройствах промышленной автоматики. Наиболее распространенными являются суммирующие и интегрирующие схемы на ОУ, а также ряд схем, в которых ОУ используются в нелинейном режиме (мультивибратор, одновибратор, ГЛИН и т.д.).
Суммирующие схемы Инвертирующий сумматор
Инвертирующий сумматор формирует алгебраическую сумму двух напряжений и меняет знак на обратный. Схема инвертирующего сумматора на два входа приведена на рис. 1.19.
Рис. 1.19. Схема инвертирующего сумматора
Для идеального ОУ при Roc = R
Uвых= -(U1+ U2).
Для n - входов
Uвых = - (U1+ U2+ ... + Un).
Суммирующие схемы могут работать как при постоянных, так и при переменных входных напряжениях.
Суммирующая схема с масштабными коэффициентами.
Если отдельным входным напряжениям надо придать различные веса, то используется схема суммирования с масштабными коэффициентами.
Рис. 1.20. Суммирующая схема с масштабными коэффициентами
Для n-входов идеального ОУ
Схема сложения-вычитания.
Схема приведена на рис. 1.21.
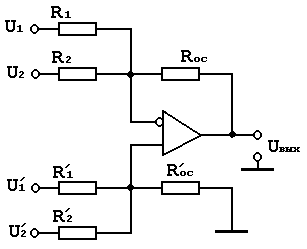
Рис. 1.21. Схема сложения-вычитания
Условия правильной работы сводятся к тому, чтобы сумма коэффициентов усиления инвертирующей части схемы была равна сумме коэффициентов усиления ее неинвертирующей части. То есть инвертирующий и неинвертирующий коэффициенты усиления должны быть сбалансированы.
Отсюда имеем:
где m - число инвертирующих входов, n - число неинвертирующих входов.
Неинвертирующий сумматор.
Рассмотрим схему на два входа:
Рис. 1.22. Неинвертирующий сумматор
В данной схеме Uвых= U1+ U2, если
и Rос' = R1' = R2'.
Можно также осуществить суммирование с весами.
Интегратор и дифференциатор
Интегратор и дифференциатор - это две схемы из числа наиболее важных аналоговых вычислительных схем. Интегратор используется в схемах управления во всех тех случаях, когда надо решать дифференциальное уравнение или надо вычислить интеграл входного сигнала. Дифференциатор используется тогда, когда надо получить выходной сигнал, пропорциональный скорости изменения входного.
Величина выходного сигнала интегратора в общем виде описывается уравнением
где Uвых(0) - начальное значение выходного сигнала в момент времени t = 0, К - коэффициент пропорциональности.
Схема простейшего интегратора на ОУ:
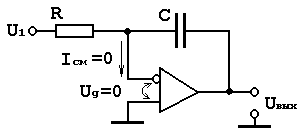
Рис. 1.23. Схема интегратора на ОУ
Для него можно получить
Схема дифференциатора создает на выходе напряжение, пропорциональное скорости изменения входного:
Рис. 1.24. Схема дифференциатора на ОУ
При дифференцировании усилитель должен пропускать только переменную составляющую входного напряжения и коэффициент усиления дифференцирующей схемы должен возрастать при увеличении скорости изменения входного сигнала.