НАДІЙНІСТЬ ТЕХНОЛОГІЧНИХ СИСТЕМ КУРС ЛЕКЦІЙ ТДАТУ
.pdf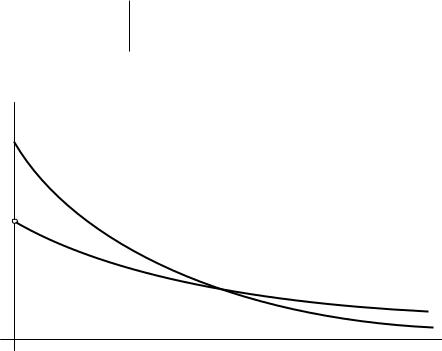
де с – параметр розподілу, який визначає положення кривої щільності розподілу на площині координат f(t) – t і має розмірність [год–1].
Криві щільності розподілу напрацювання до відмови f(t) наведено на рис. 8.
Знайдемо аналітичні вирази для розрахунків показників надійності виробів з використанням даної моделі відмов. Згідно з (1) маємо
t |
|
|
t |
|
R t 1 с exp сt dt 1 exp сt d сt |
||||
0 |
|
|
0 |
|
1 exp с t |
t |
1 |
exp с t 1 |
exp с t . |
|
||||
|
0 |
|
|
|
f(t)
(30)
c1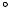 
c |
2 |
|
0
f1 (t) c1 exp( 1t)
f |
2 |
(t) c |
2 |
exp(- |
2 |
t) |
|
|
|
|
t
Рис. 8. Залежність f(t) в експоненціальній моделі відмов
Таким чином, ймовірність безвідмовної роботи елементів, виробів та систем при використанні для розрахунків експоненціальної моделі відмов визначається досить простою аналітичною залежністю (30). Проте, в цій простій залежності параметр розподілу с поки що залишається невідомим. Визначимо його, використовуючи фундаментальне співвідношення теорії надійності, яке пов’язує інтенсивність відмов зі щільністю їхнього розподілу на осі напрацювання та ймовірністю безвідмовної роботи:
131
λ t
f t R t
с exp с t c const . exp с t
(31)
Параметр с в експоненціальному розподілі чисельно дорівнює деякому константному значенню інтенсивності відмов розглянутих елементів, виробів чи систем, тобто експоненціальна модель описує відмову як явище, яке виникає зі сталою інтенсивністю = с, що, природно, обмежує область застосування моделі як з певними інтервалами напрацювання, так і для певних типів виробів.
З урахуванням (31) щільність розподілу напрацювання до відмови в експоненціальній моделі відмов
f t exp t .
(32)
Складемо розрахункові залежності для оцінювання безвідмовності на основі даної моделі відмов. Використовуючи (30), можна записати
R t exp λ t
,
(33)
а ймовірність виникнення відмови за напрацювання t:
Q t 1 exp λt .
З урахуванням (33) середнє напрацювання до відмови:
|
|
|
exp λt dt |
1 |
|
exp λt d λt |
1 |
exp λt |
|
o |
|
|
|
0 |
|||||
T |
|
|
|
|
|
|
|||
|
λ |
|
λ |
|
|||||
|
|
0 |
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
. (34)
Підставивши значення меж, остаточно отримаємо аналітичний зв'язок між параметром експоненціальної моделі
– інтенсивністю відмов і середнім напрацюванням виробу до відмови:
132
Tо
1 λ
.
(35)
Це співвідношення дозволяє знайти оцінку параметра розподілу . Для цього необхідно обчислити на основі статистичних даних ti оцінку першого початкового моменту α1* даного розподілу, вважаючи її такою, що дорівнює То. Оцінку параметра експоненціальної моделі відмов знайдемо за
залежністю |
λ |
* |
1/ α1 . |
|
|
|
|
* |
|
|
|
Істотним |
|
обмеженням |
для |
застосування |
|
експоненціального розподілу як моделі відмов є неможливість урахування розсіювання напрацювання виробу до відмови. Для цього запишемо аналітичний вираз для дисперсії напрацювання до відмови, що, за визначенням, є другим центральним моментом випадкової величини t:
D t |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
||
|
о |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
f t dt |
|
t |
|
λexр λt dt |
|
|||||||||||
|
t T |
|
|
λ |
|
||||||||||||
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
exp λt dt |
|
|
texp λt dt |
|
|
exp λt dt . |
|||||||||
λ t |
λ |
λ |
2 |
||||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
||
(36)
Обчислимо перший інтеграл (у квадратних дужках (36)), застосувавши інтегрування вроздріб. Введемо позначення:
u t |
2 |
; |
du 2tdt; |
dv exp λt dt; |
|||||
|
|||||||||
Тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
2 |
|
I1 t 2 exp λt dt uv |
|
v du |
|
exp λt |
|||||
|
λ |
||||||||
0 |
|
|
|
0 |
0 |
|
|
||
|
|
|
|
|
|
|
|||
v
0
1 exp λt
λ
2 |
|
|
t exp λt dt. |
||
λ |
||
0 |
||
|
.
(37)
Перший доданок у цьому виразі при підстановці верхньої межі перетворюється на нуль, оскільки exp(λt) збільшується швидше, ніж t 2 ; другий доданок скорочується з аналогічним виразом у (7) зі знаком „–“. Остаточно одержуємо:
133
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||
D t λ |
λ |
2 |
exp λt dt |
λ |
2 |
exp λt d λt |
||||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
||||||
|
1 |
[exp( λt) |
|
] |
1 |
[0 1] |
1 |
. |
||||||||
λ |
2 |
0 |
λ |
2 |
λ |
2 |
||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(38)
Середнє |
квадратичне відхилення |
напрацювання до |
||
відмови від |
центра розсіяння То: |
σ |
D[t] 1 |
, тобто |
|
|
|||
дорівнює значенню середнього напрацювання То, внаслідок чого коефіцієнт варіації напрацювання до відмови в експоненціальній моделі відмов завжди дорівнює одиниці:
ν Т |
о =1. |
|
Аналогічно можна показати, що фіксованим є не тільки другий, але також третій і четвертий моменти експоненціального розподілу (коефіцієнт асиметрії завжди дорівнює двом, коефіцієнт ексцесу – дев'яти). Це змушує дослідників користуватись тільки математичним сподіванням, тоді як показники безвідмовності істотно залежать від розсіяння (розкиду) напрацювання.
Особливість цієї моделі відмов обумовлена її простотою. Для цього знайдемо аналітичний вираз для параметра потоку відмов (t) і запишемо зображення за Лапласом щільності експоненціального розподілу напрацювання до відмови (32):
f s
λ λ s
.
(39)
Підставивши |
|
s у |
вираз, одержимо зображення за |
||||||
f |
|||||||||
Лапласом для параметра потоку відмов: |
|
|
|||||||
|
|
|
|
|
λ (λ s) |
λ |
|||
|
|
|
|
|
|||||
|
|
ω(s) |
|
|
|
. |
|||
|
|
1 λ λ s |
s |
||||||
Оригіналом цього зображення є
(t) = = const. (40)
Таким чином, в експоненціальній моделі відмов параметр потоку відмов не залежить від напрацювання і чисельно
134
дорівнює значенню параметра розподілу (інтенсивності відмов). Через цей збіг показників деякі фахівці у своїх дослідженнях ототожнюють “інтенсивність відмов” (показник безвідмовності невідновлюваних виробів) з “параметром потоку відмов” (показником безвідмовності відновлюваних виробів), не враховуючи того, що насправді емпіричні (реальні) характеристики цих показників мають зовсім різні закономірності у часі.
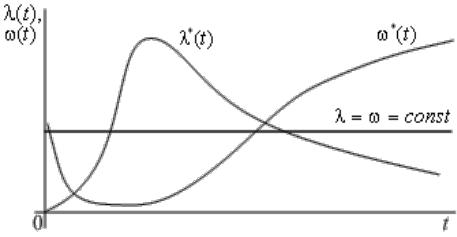
Рисунок 9 ілюструє співвіднесеність емпіричних залежностей інтенсивності відмов і параметра потоку відмов від напрацювання з теоретичними залежностями, які випливають із експоненціальної моделі відмов зі щільністю розподілу.
Ця ілюстрація наочно показує, що експоненціальний розподіл є досить „грубою“ моделлю розподілу відмов, що „вирівнює“ принципово різні показники – емпіричні *(t) і*(t). Методика одержання статистичних даних для оцінювання інтенсивності відмов *(t) принципово відрізняється від умов одержання статистики відмов для оцінки параметра потоку відмов *(t). Експоненціальна модель відмов „не дозволяє розрізняти“ середнє напрацювання до відмови То (показник безвідмовності невідновлюваних систем) і середнє напрацювання на відмову Т1 (показник безвідмовності відновлюваних систем), оскільки:
Т1 = 1/ = 1/ = То.
135
Рис. 9. Емпіричні залежності *(t) і *(t) та параметр = експоненціальної моделі розподілу відмов
Експоненціальний розподіл був першою моделлю відмов, на основі якої розраховувалася безвідмовність елементів і технічних систем з самого початку появи теорії надійності як науки (середина ХХ ст.). Багато вчених і фахівців–практиків віддають перевагу цій моделі відмов завдяки її простоті, оскільки однопараметрична модель спрощує розв’язання задач надійності. Достатньо сказати, що всі оптимізаційні задачі у галузі надійності вирішувались з використанням тільки експоненціальної моделі. І модель виправдала своє призначення, адекватно відображаючи статистику відмов елементної бази, яку використовували в технічних системах у 1950–1970 роках. Це спричинило досить істотний зсув вправо (по осі напрацювання) середнього значення (математичного сподівання) статистичного напрацювання до відмови То, внаслідок чого експоненціальний розподіл найчастіше не узгоджувався з реальною статистикою відмов.
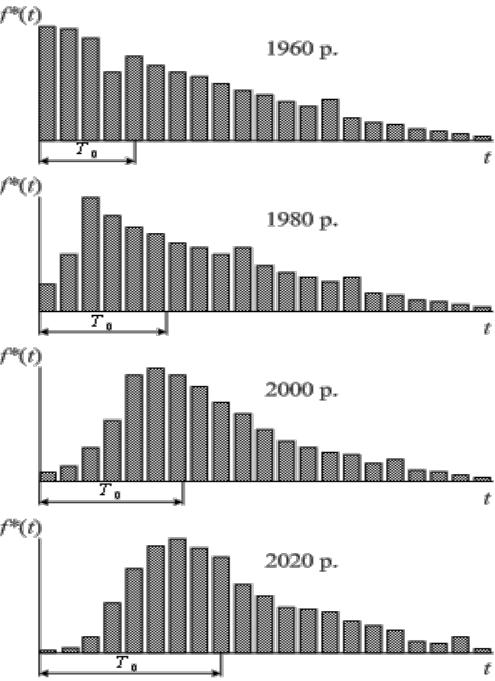
Якісну динаміку (послідовне збільшення) середнього напрацювання до відмови з підвищенням надійності елементної бази наведено на рис. 10 у вигляді гістограм f*(t), які відповідають двадцятирічним періодам розвитку техніки і технологій. Практика змушує рахуватись з тим, що розподіл напрацювання до відмови високонадійної елементної бази має одномодальну форму, тому двопараметричний розподіл є більш адекватною функцією, здатною добре, гнучко апроксимувати подібну статистику.
Підстав вважати, що статистика буде іншою, немає. Спроби „підігнати“ розрахункові показники безвідмовності систем, які отримані на основі експоненціального розподілу відмов, під реальні значення, що досягаються при експлуатації, за допомогою емпіричних коефіцієнтів говорять, природно, не на користь цієї моделі відмов.
Стала інтенсивність відмов у експоненціальній моделі надійності означає, що експоненціальний розподіл ніяк не враховує старіння, знос та інші деградаційні процеси, тобто
136
виключає необхідність застосування якісніших матеріалів під час виробництва виробів або проведення профілактичних робіт в процесі експлуатації.
Щільність розподілу відмов у цій моделі максимальна в початковий період експлуатації, отже, модель відображає недосконалу технологію і якість проектування, виготовлення і складання.
Рис. 10. Динаміка безвідмовності Tо* елементної бази
137
6.4 Закон розподілу Вейбулла
Основні характеристики розподілу Вейбулла
Розподіл Вейбулла – двопараметричний закон розподілу випадкового напрацювання до відмови з параметрами: 0, що визначає масштаб, і k, що визначає асиметрію. Розподіл Вейбулла широко використовується для визначення показників надійності ТС, при дослідженні їх міцності і довговічності. Ним описується інтенсивність відмов на всьому проміжку експлуатації ТС.
Розподіл Вейбулла був отриманий емпірично в результаті аналізу великої кількості розподілів ресурсів і відповідає ситуації руйнування самої слабкої ланки (елемента) з деякої сукупності (системи, яка складається з окремих елементів).
Розподіл Вейбулла характеризується такими функціями
(рис. 11):
– ймовірністю безвідмовної роботи:
P t e |
t |
m |
t |
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
–інтенсивністю відмов:
t m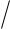
t0 tm 1
– щільністю розподілу:
f t |
m |
|
|
t |
m |
t |
|
|
t |
m 1 |
|
0 |
|||||
|
|
e |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
t |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(41)
(42)
(43)
Розподіл Вейбулла також має два параметри: параметр форми m > 0 і масштабний параметр t0 > 0.
Математичне сподівання і середнє квадратичне відхилення визначають відповідно:
mt Bmt01/ m ;
S |
|
Cmt |
1/ m |
|
t |
0 |
|||
|
|
(44)
де Bm і Cm – коефіцієнти.
Якщо протягом певного часу t' відмови не відбуваються, то імовірність безвідмовної роботи визначають за формулою:
138
P t e |
m |
t |
|
t t |
|
|
|
0 |
Іноді характеристики розподілу Вейбулла використанням інших позначень. Наприклад, безвідмовної роботи можна подати так:
(45)
записують з імовірність
|
|
|
|
|
|
|
|
|
|
|
t a |
|
|
|
|
|
|
|
|
|
|
P t e |
b |
|
|
||
|
b m |
|
a t |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
де |
|
|
|
і |
|
1 m |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
Можливості та універсальність закону Вейбулла очевидні |
|||||||||||||
з рис. 11. |
|
|
|
|
|
t |
|
f t |
|
|
|
||
При m < 1 функції |
і |
спадаючі. |
|
||||||||||
|
|
|
|
||||||||||
При m = 1 розподіл перетворюється на експоненціальний з |
|||||||||||||
λ t соnst |
і |
f |
t |
─ спадна функція. |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
Якщо m > 1 функція |
f t |
має вершину, як у логарифмічно |
|||||||||||
|
|
||||||||||||
нормальному |
|
розподілі, |
то |
функція |
λ t |
є безперервно |
|||||||
|
|
||||||||||||
зростаючою і при 1 < m < 2 випуклою, а при m > 2 – увігнутою. |
||
За умови m = 2 функція |
λ t |
лінійна у розподілі Вейбулла |
|
||
перетворюється на відомий розподіл Релея.
Якщо m = 3,3, то розподіл Вейбулла близький до нормального.
Графічне оброблення результатів випробувань з використанням розподілу Вейбулла проводять у такому
порядку: |
|
|
|
|
– |
логарифмують |
функцію |
надійності |
|
lg P t tm |
t |
0,4343 |
|
|
|
0 |
; |
|
|
– вводять позначення y lg P t ; |
|
|||
– логарифмують |
lg y |
|||||
|
|
|||||
де |
A lg t |
0 |
0,362 |
. |
||
|
|
|
|
|||
Відклавши |
результати |
|||||
координатами |
|
lg t lg y |
(див. |
|||
m lg t A ;
випробувань на графіку з рис. 11) і, з’єднавши отримані
точки прямою, матимемо |
m tgα |
|
нахилу прямої до осі абсцис; А – на осі ординат.
; lgt0 A 0,362 , де α – кут відрізок, який відсікає пряма
139
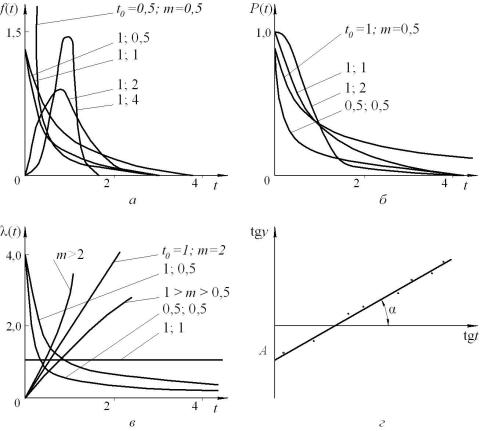
Рис. 11. Характеристики розподілу Вейбулла:
а – щільність розподілу; б – функція надійності; в – інтенсивність відмов; г – графічне визначення параметрів
розподілу
Розподіл Вейбулла досить універсальний. Він задовільно описує напрацювання до відмови деталей машин, які руйнуються від утоми.
Розподіл Вейбулла є досить гнучкою функцією, здатною добре вирівнювати різноманітну статистику відмов, і може бути моделлю відмов, в основному, – механічних виробів.
140