Глава 2. Интегральное исчисление

Содержание:

Тема 2.1. Неопределённый интеграл 2

Первообразная функция и неопределенный интеграл 2

Свойства неопределенного интеграла. 3

Интегралы от основных элементарных функций. 4

Методы интегрирования. 4

Тема 2.2. Определённый интеграл 5

Понятие определенного интеграла, его геометрический смысл 5

Формула Ньютона—Лейбница 7

Тема 2.3. Обыкновенные дифференциальные уравнения 8

Дифференциальные уравнения первого порядка 8

Определение дифференциального уравнения первого порядка. 8

Решение уравнения. 8

Общее и частное решение уравнения. 8

Уравнения с разделяющимися переменными. 9

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 9

Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу — нахождение самой функции по ее производной или дифференциалу.

Тема 2.1. Неопределённый интеграл Первообразная функция и неопределенный интеграл

Определение. Функция F[x) называется первообразной функцией для функции f(x) на промежутке X, если в каждой точке х этого промежутка F'(x)=f(x).

Например, F(x)= является первообразной для функции f(x)=x², так как

.

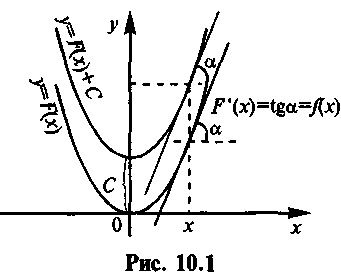
По геометрическому смыслу производной F'(x) есть угловой коэффициент касательной к кривой y=F(x) в точке с абсциссой х. Геометрически найти первообразную для f(x) - значит найти такую кривую y=f[x), что угловой коэффициент касательной к ней в произвольной точке х равен значению f(x) заданной функции в этой точке (см. рис. 10.1).

Следует отметить, что для заданной функции f(x) ее первообразная определена неоднозначно. Дифференцируя, нетрудно убедиться, что функции и вообще где С - некоторое число, являются первообразными для функции f(x)=х². Аналогично, в общем случае, если F(x) — некоторая первообразная для f(x), то, поскольку (F(x)+С) '= F'(x)=f(x), функция вида F(x)+ С, где С — произвольное число, также являются первообразными для f(x).

Геометрически это означает, что если найдена одна кривая y=F(x), удовлетворяющая условию F'(x)=tg а=f(x), то, сдвигая ее вдоль оси ординат, мы вновь получаем кривые, удовлетворяющие указанному условию (поскольку такой сдвиг не меняет углового коэффициента касательной в точке с абсциссой х) (см. рис. 10.1).

Остается вопрос, описывает ли выражение вида F(x)+C все первообразные для функции f(x). Ответ на него дает следующая теорема.

Теорема. Если F₁(x) и F₂(x) — первообразные для функции f(х) в некотором промежутке X, то найдется такое число С, что справедливо равенство

F₂(x)=F₁(x)+C.

Из данной теоремы следует, что, если F(x) — первообразная для функции f(x), то выражение вида F(x)+ С, где С — произвольное число, задает все возможные первообразные для f(x).

Определение. Совокупность всех первообразных для функции f(x) на промежутке X называется неопределенным интегралом от функции f(x) и обозначается где - знак интеграла, f(x) — подынтегральная функция, f(x)dx — подынтегральное выражение. Таким образом,

(*)

где F(x) — некоторая первообразная для f(x), С — произвольная постоянная.

Например, поскольку первообразная для функции f(x)=х², то

Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.

Свойства неопределенного интеграла.

Рассмотрим основные свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции, т.е.

Дифференцируя левую и правую части равенства (*), получаем:

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.

(**)

По определению дифференциала и свойству 1 имеем

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

(**)

где С — произвольное число.

Рассматривая функцию F(x) как первообразную для некоторой функции f(x), можно записать

и на основании (**) дифференциал неопределенного интеграла f(x)dx=dF(x), откуда

Сравнивая между собой свойства 2 и 3, можно сказать, что операция нахождения неопределенного интеграла и дифференциала взаимнообратны (знаки d и взаимно уничтожают друг друга, в случае свойства 3, правда, с точностью до постоянного слагаемого).

4. Постоянный множитель можно выносить за знак интеграла, т.е.

(****)

где а — некоторое число.

5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.

(*****)